Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 6.Exercício - Ex. 27

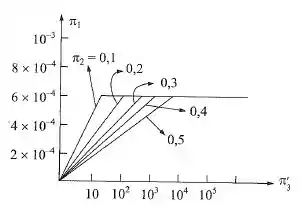
Num fenômeno, a função representativa é dada por f Q G , g , γ , v , L , μ = 0 ( Q G = vazão em peso; L = comprimento característico). Ao determinar os adimensionais pelo teorema dos π , usando a base γ , v , L , sendo π 1 = f Q G ,   π 2 = f ( g ) e π 3 ' = 1 π 3 = f μ , obteve-se o gráfico a seguir.

a) Determinar as equações dimensionais de todas as grandezas.

b) Determinar os números adimensionais.

c) Numa certa experiência, γ = 10 4   N / m 3 , v = 10   m / s , L = 5   m ,   g = 10   m / s 2 , μ = 10 - 3   N . s / m 2 . Qual é a vazão em peso em N / s ?

d) Pode-se afirmar que o efeito da viscosidade é desprezível? Em que condições?

e) Se os dados do item (c) correspondem a um modelo, qual é a escala das vazões em peso com um protótipo que é ensaiado com o mesmo fluido e que tem escala geométrica 1/16?

Passo 1

O primeiro passo é identificar a função representativa, nesse caso, o enunciado já nos forneceu.

f Q G , g , γ , v , L , μ = 0

Agora vamos escrever a equação dimensional para cada uma das grandezas:

γ = M L - 2 T - 2 ; v = L T - 1 ; L = L ; μ = M L - 1 T - 1 ; Q G = M L T - 3 ; g = L T - 2

Passo 2

Agora vamos calcular o número de adimensionais independentes m = n - r , nesse caso temos:

n = 6   g r a n d e z a s   e n v o l v i d a s   n o   f e n ô m e n o

r = 3   n ú m e r o   d e   g r a n d e z a s   f u n d a m e n t a i s   d o   f e n ô m e n o

Sendo assim, temos:

m = 6 - 3 → m = 3   ( g r u p o s   d i m e n s i o n a i s )

Agora vamos construir os números adimensionais:

π 1 = γ α 1 v α 2 L α 3 Q G

π 2 = γ β 1 v β 2 L β 3 g

π 3 = γ δ 1 v δ 2 L δ 3 μ

Agora, substituindo cada uma das grandezas dimensionais nas equações, temos:

π 1 = γ α 1 v α 2 L α 3 μ = M L - 2 T - 2 α 1 L T - 1 α 2 L α 3 M L T - 3

Então, para que π 1 seja adimensional, temos:

α 1 + 1 = 0 → α 1 = - 1

- 2 α 1 - α 2 - 3 = 0 → - 2 - 1 - α 2 - 3 → α 2 = - 1

- 2 α 1 + α 2 + α 3 + 1 = 0 → - 2 - 1 + - 1 + α 3 + 1 = 0 → α 3 = - 2

Dessa forma, temos então:

π 1 = γ - 1 v - 1 L - 2 Q G → π 1 = Q G γ v L 2

Agora, repetindo o processo para π 2 :

π 2 = γ β 1 v β 2 L β 3 g = M L - 2 T - 2 β 1 L T - 1 β 2 L β 3 L T - 2

Então, para que π 2 seja adimensional, temos:

β 1 + 0 = 0 → β 1 = 0

- 2 β 1 - β 2 - 2 = 0 → - 2 0 - β 2 - 2 = 0 → β 2 = - 2

- 2 β 1 + β 2 + β 3 + 1 = 0 → - 2 0 + ( - 2 ) + β 3 + 1 = 0 → β 3 = 1

Dessa forma, temos então:

π 2 = γ 0 v - 2 L 1 g → π 2 = L g v 2

Agora vamos encontrar π 3 :

π 3 = γ δ 1 v δ 2 L δ 3 μ = M L - 2 T - 2 δ 1 L T - 1 δ 2 L δ 3 M L - 1 T - 1

Então, para que π 3 seja adimensional, temos:

δ 1 + 1 = 0 → δ 1 = - 1

- 2 δ 1 - δ 2 - 1 = 0 → - 2 - 1 - δ 2 - 1 = 0 → δ 2 = 1

- 2 δ 1 + δ 2 + δ 3 - 1 = 0 → - 2 - 1 + 1 + δ 3 - 1 = 0 → δ 3 = - 2

Dessa forma, temos então:

π 3 = γ - 1 v 1 L - 2 μ → π 3 = v μ γ L 2

Passo 3

Agora para a letra c), vamos usar os dados fornecidos e os adimensionais encontrados no passo 2, começando por π 2 :

π 2 = L g v 2

Substituindo os valores conhecidos:

π 2 = 5 10 10 2 → π 2 = 0,5

Agora vamos calcular π 3 ' :

π 3 ' = 1 π 3 → π 3 ' = γ L 2 v μ

Substituindo os valores conhecidos:

π 3 ' = 10 4 5 2 10 10 - 3 → π 3 ' = 2,5.10 7

Agora, usando os pontos π 2 e π 3 ' no gráfico fornecido no enunciado, encontramos um valor de π 1 :

π 1 = 6.10 - 4

E, com isso, conseguimos encontrar a vazão para o sistema através do primeiro adimensional:

π 1 = Q G γ v L 2

Substituindo os valores conhecidos:

6.10 - 4 = Q G 10 4 10 5 2 → Q G = 1500   N / s

Passo 4

Para responder a letra d), basta que analisemos o adimensional π 3 ' no gráfico fornecido, esse é o adimensional calculado levando em conta as forças viscosas ( μ ) , e conforme podemos ver no gráfico, a partir de um certo valor, ele se torna constante, logo, pode-se desprezar o efeito da viscosidade para altos valores de π 3 ' , analisando a equação para π 3 ' :

π 3 ' = γ L 2 v μ

Então, qualquer um desses termos que faça com que π 3 ' seja muito alto, faz com que possamos desprezar o efeito da viscosidade.

Passo 5

Para resolver um problema entre modelo e protótipo, sabemos que para ter semelhança, os adimensionais devem ser iguais, nesse caso, pelas condições do enunciado, sabemos que:

γ p = γ m ;   L m = 16 L p ; g p = g m

Nesse caso, analisando o adimensional π 2 :

π 2 m = π 2 p → L m g v m 2 = L p g v p 2 → 16 L p v m 2 = L p v p 2 → v p v m = 1 16 → v p v m = 1 4

Agora, analisando π 1 , temos:

π 1 m = π 1 p → Q G m γ m v m L m 2 = Q G p γ p v p L p 2 → Q G p Q G m = v p v m L p L m 2

Substituindo os valores conhecidos:

Q G p Q G m = 1 4 L p 16 L p 2 → Q G p Q G m = 1 1024

Resposta

γ = M L - 2 T - 2 ; v = L T - 1 ; L = L ; μ = M L - 1 T - 1 ; Q G = M L T - 3 ; g = L T - 2

π 1 = Q G γ v L 2 ; π 2 = L g v 2 ; π 3 = v μ γ L 2

Q G = 1500   N / s

Q G p Q G m = 1 1024

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre um conjunto adequado de parâmetros adimensionais para organizar dados oriundos de uma experiência de laboratório, na qual um tanque é drenado através de um orifício a partir de um nível inici
Medições da altura de líquido a montante de uma obstrução colocada em um escoamento de canal­ aberto podem ser usadas para determinar a vazão em volume. (Tais obstruções, projetadas e calibradas para
O tempo, t , para drenagem de óleo para fora de um recipiente de calibração de viscosidade depende da viscosidade, μ , e massa específica, ρ , do fluido, do diâmetro do orifício, d , e da aceleração d
Uma correia continua, movendo verticalmente através de um banho de líquido viscoso, arrasta uma camada de líquido de espessura h ao longo dela. Considere que a vazão volumétrica de líquido, Q , depend
No exemplo 5.1 usamos o teorema de pi para desenvolver a equação 5.2 com base na equação 5.1. Em lugar de simplesmente listar as dimensões de cada variável, alguns pesquisadores listam as potências de