Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 32
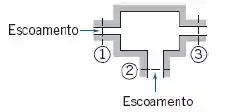
No escoamento incompressível através do dispositivo mostrado, as velocidades podem ser consideradas uniformes em todas as seções de entrada e de saída. As seguintes condições são conhecidas: , , , e ( em segundos). Obtenha uma expressão para a velocidade na seção e trace um gráfico de como uma função do tempo. Em que instante torna-se zero pela primeira vez? Qual é a vazão volumétrica total média na seção ?
Passo 1
Nos foi dado no enunciado que:
Passo 2
Temos que considerar que o regime é permanente, o fluido é incompressível, e a velocidade em cada entrada e saída é uniforme. Assim, temos que a equação da continuidade se torna a seguinte:
Considerando o dispositivo mostrado temos o seguinte:
Passo 3
Temos também que examinar a cada termo da equação acima e as direções dos vetores. Em o vetor velocidade e o vetor área agem em direções opostas.
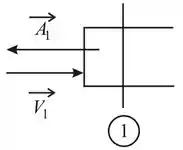
Portanto, o sinal de é negativo. Assim .
Passo 4
Em o vetor velocidade e o vetor área agem em direções opostas.
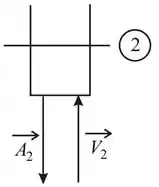
Portanto, o sinal de é negativo. Assim .
Passo 5
Em o vetor velocidade e o vetor área agem na mesma direções.
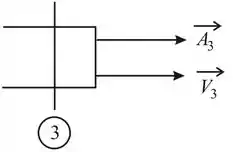
Portanto, o sinal de é positivo. Assim .
Passo 6
Assim, temos que a equação da continuidade fica da seguinte forma:
Queremos encontrar uma expressão para , então podemos rescrever o equação da seguinte forma:
Podemos agora substituir os dados fornecidos no enunciado.
Passo 7
Usando a expressão acima, o gráfico de em função do tempo ficou da seguinte maneira.
Passo 8
A partir do gráfico, podemos observar que se torna zera a primeira vez quando é igual a segundos.
Passo 9
Podemos calcular o fluxo volumétrico médio com a seguinte expressão:
Quando limite tende ao infinito, o termo entre tende a zero. Assim, temos que:
Portanto o fluxo volumétrico médio é .