Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 37

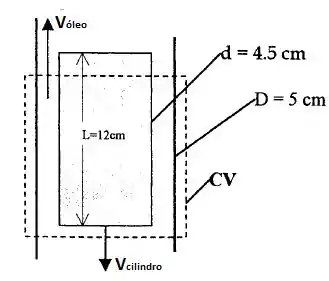
Um cilindro sólido de aço de 4,5 cm de diâmetro e 12 cm de comprimento, com massa de 1500g, cai concentricamente por uma cuba vertical de 5 cm de diâmetro cheia de óleo (d = 0,89). Considerando o óleo incompressível, calcule sua velocidade média na folga anular entre o cilindro e a cuba (a) relativa à cuba e (b) relativa ao cilindro.

Passo 1

(a) Se você observar bem ali meu jovem, você verá que fixamos um volume de controle CV em torno do container. A gente sabe que pelo balanço de massa, considerando um escoamento incompressível, teremos o termo transiente sendo anulada e por fim, nosso balanço de massa será:

Q c i l i n d r o = Q ó l e o

A c i l i n d r o V c i l i n d r o = A ó l e o V ó l e o

Observe algo interessante aqui, a região por onde o óleo escoará é na verdade dado pela diferença dos diâmetros maior e menor, concorda comigo?

π 4 d 2 V c i l i n d r o = π 4 D 2 - d 2 V ó l e o

V ó l e o = d 2 D 2 - d 2 V c i l i n d r o = 0,045 2 0,05 2 - 0,045 2 V c i l i n d r o = 4,26 V c i l i n d r o

Passo 2

(b) Agora se o nosso volume de controle começar a se mover com o cilindro, a gente vai obter a velocidade relativa ao cilindro, concorda?

V ó l e o   r e l a t i v o   a o   c i l i n d r o = V a + V c i l i n d r o

Onde V a é a velocidade que encontramos na letra (a) e quem será nossa velocidade do cilindro, temos que:

V ó l e o   r e l a t i v o   a o   c i l i n d r o = V a + V c i l i n d r o = D 2 D 2 - d 2 V c i l i n d r o = 5,26 V c i l i n d r o

Resposta

  1. V ó l e o = 4,26   V c i l i n d r o
  2. V ó l e o   r e l a t i v o   a o   c i l i n d r o = 5,26   V c i l i n d r o
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema da figura, tem-se um único fluido incompressível de v = 10 - 4 m 2 / s e ρ = 1000k g / m 3 .Qual é o número de R e nas seções 1 e 4 ?Qual é a velocidade média na seção ( 2 ) ( m / s ) ?Qual
O filtro de admissão de combustível de uma certa máquina é formado por um elemento poroso com forma de tronco de cone. O com 10L / s . A distribuição de velocidades na face superior é linear com v m á
O campo de velocidades de um escoamento é dado por v x = 3 y e v y = 2 .O movimento é variado ou permanente?Determinar o campo das acelerações.Determinar os módulos da velocidade e aceleração no ponto
A placa da figura tem uma área de 2m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa formando um diagrama de velocidades bidimensional dado por v = 20 y v m á x ( 1 - 5 y
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. No sistema da figura, o óleo fornecido pela bomba mantém o pistão parado. O óleo escoa através da folga entre o pistão e