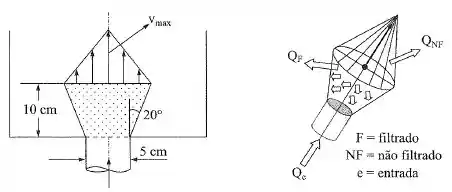
O filtro de admissão de combustível de uma certa máquina é formado por um elemento poroso com forma de tronco de cone. O com. A distribuição de velocidades na face superior é linear com . Qual é a vazão de combustível que será filtrada pela parede porosa?

Para começarmos a resolver a questão, podemos utilizar semelhança de triângulos para encontrarmos o perfil de velocidade, olha só:

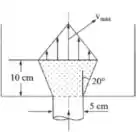
Temos uma velocidade máxima que se relaciona com o raio maior, e uma velocidade () que se relaciona com o raio da parte central da imagem… Olhando a figura podemos dizer que esse raio da parte central seria o raio maior menos o raio menor, portanto, ficamos com:

E isolando a velocidade, temos:

Lembrando que a variação infinitesimal da área será dada por:

Podemos então, encontrar a vazão da parte não filtrada, substituindo o perfil de velocidade encontrado e a variação de área:

Separando as constantes da integral, temos que:

Resolvendo, temos que:

Fazendo a substituição dos limites, temos:

Aplicando a distributiva:

Ajustando essa galera aí, teremos:

E ficaremos com:

Precisamos do valor de , né? E podemos encontrar ele analisando geometricamente o sistema, olha só:

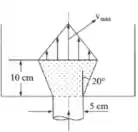
O raio , será dado pelo raio da parte menor, que será a metade do valor de diâmetro dado, mais o comprimento do tronco de cone vezes a tangente do ângulo que ele forma… ou seja, teremos que:

Beleza! Temos então:

Show! Agora podemos encontrar a vazão não filtrada, substituindo os valores na equação:

Ficamos com uma vazão não filtrada de:

Ou:

Agora sim podemos encontrar a vazão filtrada! Usando a lei de conservação que vimos lá no comecinho, temos que:

Substituindo os valores:

A vazão da parte filtrada, será então: