Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 14

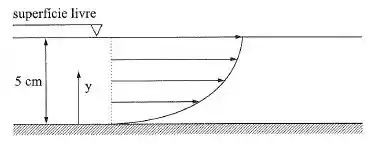
O esquema a seguir corresponde à seção longitudinal de um canal de 25   c m de largura. Admitindo escoamento bidimensional e sendo o diagrama de velocidades dado por v = 30 y - y 2 ( y   e m   c m ; v   e m   c m / s ) , bem como o dluido de peso específico: 0,9   N / L e viscosidade cinemática: 70   c S t e g = 10   m / s 2 , determinar:

  1. o gradiente de velocidade para y = 2   c m ;
  2. a máxima tensão de cisalhamento na seção ( N / m 2 ) ;
  3. a velocidade média na seção em c m / s .
  4. a vazão em massa na seção.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A viscosidade cinemática será:

v = 0,7   S t

Como S t = c m 2 / s , temos que:

v = 0,7   c m 2 / s

v = 7 ⋅ 10 - 5   m 2 / s

O peso específico no S I será:

γ = 9 ⋅ 10 4   N / m 3

O gradiente da velocidade é dado por:

d v d y = 30 - 2 y

Como queremos para y = 2   c m , temos que:

d v d y = 26   s - 1

Passo 2

A tensão de cisalhamento será máxima onde o gradiente for máximo:

τ m á x = μ d v d y m á x

A viscosidade dinâmica não foi dada mas sabemos que:

μ = v ρ

Porém a massa específica também não foi dada, porém:

ρ = γ g

Logo:

τ m á x = v γ g 30 - 2 y y = 0

Portanto:

τ m á x = 0,189   P a

Passo 3

A equação para a velocidade média é:

v m = 1 A ∫ v d A

Logo:

v m = 1 b h ∫ 0 h 30 y - y 2 b d y

Resolvendo a integral, temos que:

v m = 1 h 30 y 2 2 - y 3 3 0 h

v m = 66,7   c m / s

Passo 4

A vazão mássica é dada por:

Q m = ρ v m A

Portanto:

Q m = γ g v m A

Resolvendo, temos que:

Q m = 0,75   k g / s

Resposta

a )   d v d y = 26   s - 1

b )   τ m á x = 0,189   P a

c )   v m = 66,7   c m / s

d )   Q m = 0,75   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Óleo escoa em regime permanente formando uma fina camada em um plano inclinado para baixo. O perfil de velocidade é dado por: Expresse a vazão mássica por unidade de largura em termos de ρ , μ , g , θ
Normas para ventilação de ar em salas de aula especificam uma renovação do ar da sala com uma vazão de pelo menos 8,0L / s de ar fresco por pessoa (estudantes e professor). Um sistema de ventilação pa
Um fluido incompressível escoa em regime permanente por meio de um canal plano divergente. Na seção de entrada, de altura H , o escoamento é uniforme com módulo V 1 . Na saída, de altura 2 H , o perfi
Água entra em um canal largo e plano, de altura 2h, com uma velocidade de 2,5m / s . Na saída do canal, a distribuição de velocidades é dada por u u m á x = 1 - y h 2 á em que y é medido a partir da l
No escoamento incompressível através do dispositivo mostrado, as velocidades podem ser consideradas uniformes em todas as seções de entrada e de saída. As seguintes condições são conhecidas: A 1 = 0,1