Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 18

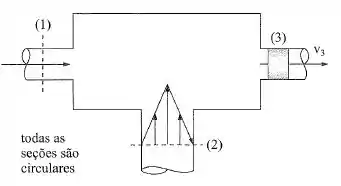
No sistema da figura, A 3 = 0,5   m 2 , ρ 3 = 0,4   k g / m 3 e os fluidos são gases. Dados:

Seção ( 1 ) : v = 4 1 - r R 2 ; Q 1 = 2   m 3 / s ; ρ 1 = 0,6   k g / m 3

Seção ( 2 ) : v = 9 1 - r 0,4 ; ρ 2 = 1,2   k g / m 3

Determinar:

  1. A velocidade do pistão;
  2. O raio da seção 1 ;
  3. A mínima viscosidade dinâmica do fluido na seção 1 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Sabemos que:

v m 2 A = ∫ v 2 d A

Desenvolvendo, temos que:

v m 2 π R 2 2 = ∫ 0 R v m á x 1 - r R d A

v m 2 π R 2 2 = v m á x ∫ 0 R R - r R d A

v m 2 π R 3 = v m á x ∫ 0 R ( R - r ) 2 π r d r

Resolvendo, temos que:

v m 2 R 3 = 2 v m á x R r 2 2 - r 3 3 0 R

v m 2 R 3 = 2 v m á x R 3 6

Logo:

v m 2 = v m á x 3

v m 2 = 9 3 = 3   m / s

Passo 2

Vamos avaliar o perfil na seção 2 . Quando r = R 2 , temos que v = 0 , portanto:

9 1 - R 2 0,4 = 0

R 2 = 0,4   m

Agora podemos encontrar a vazão mássica em 2 :

Q m 2 = ρ 2 v m 2 A 2

Q m 2 = ρ 2 v m 2 π R 2 2

Q m 2 = 1,8   k g / s

A vazão mássica em 1 também pode ser encontrada por:

Q m 1 = ρ 1 Q 1

Q m 1 = 0,6 2

Q m 1 = 1,2   k g / s

Aplicando a equação da continuidade, temos que:

Q m 3 = 1,8 + 1,2

Q m 3 = 3   k g / s

Sendo assim, a velocidade média no pistão v m 3 será:

Q m 3 = ρ 3 v m 3 A 3

v m 3 = 3 0,4 0,5

v m 3 = 15   m / s

Passo 3

Para o item “b” sabemos que de acordo com a equação apresentada no enunciado para a velocidade da seção 1 , o escoamento é laminar, portanto:

v m 1 = v m á x 2

v m 1 = 2   m / s

Podemos então encontrar o raio da seção 1 :

Q 1 = v m 1 A 1

Q 1 = v m 1 π R 1 2

2 = 2 π R 1 2

R 1 = 0,564   m

Passo 4

Para que o escoamento seja laminar, temos que:

R e ≤ 2000

Como:

R e = μ 1 v m 1 D 1 ρ 1

Temos que:

2000 = μ 1 v m 1 D 1 ρ 1

2000 = μ 1 2 ( 2 ⋅ 0,564 ) 0,6

μ 1 = 6,77 ⋅ 10 - 4   P a ⋅ s

Resposta

a ) v m 3 = 15   m / s  

b ) R 1 = 0,564   m

c ) μ 1 = 6,77 ⋅ 10 - 4   P a ⋅ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque, com volume de 0,4m 3 , contém ar comprimido. Uma válvula é aberta e o ar escapa com velocidade de 250m / s através de uma abertura de 100m m 2 de área. A temperatura do ar passando pela abe
Água é drenada de um tanque cilíndrico, de 0,3m de diâmetro, através de um orifício no fundo do tanque. No instante em que a profundidade da água é 0,6m , a vazão em massa observada no dreno é 4k g /
Água entra em um canal bidimensional de largura constante, h = 75,5m m , com velocidade uniforme, U . O canal faz uma curva de 90 º º que distorce o escoamento de modo a produzir, na saída, o perfil l
Em uma notícia divulgada recentemente na TV sobre o abaixamento do nível do lago Shafer perto de Monticello, Indiana, pelo aumento na descarga através da comporta do lago, as seguintes informações for
Para o funil do Problema 4.55 , determine o diâmetro d requerido se o funil é drenado em t = 1m i n para uma profundidade inicial y 0 = 30c m . Trace o gráfico do diâmetro d requerido para drenar o fu