Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 13

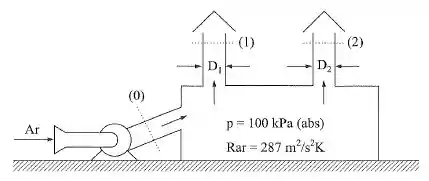
O insuflador de ar da figura gera 16.200   m 3 / h na seção ( 0 ) com uma velocidade média de 9,23   m / s . Foram medidas as temperaturas nas seções 0 ,   ( 1 ) e ( 2 ) , sendo, respectivamente, t 0 = 17 ° C ; t 1 = 47 ° C e t 2 = 97 ° C . Admitindo como imposição do projeto do sistema que o número de Reynolds nas seções 1 e 2 deva ser 1 0 5 e sabendo que diâmetro D 2 = 80   c m , v a r = 8 × 10 - 5   m 2 / s e que a pressão tem variação desprezível no sistema, determinar:

  1. O diâmetro da seção 1 ;
  2. As vazões em volume em 1 e 2 ;
  3. As vazões em massa em 1 e 2 .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A vazão na seção ( 0 ) é de:

Q 0 = 16200   m 3 / h

Q 0 = 16200 m 3 h ⋅ h 3600   s

Q 0 = 4,5   m 3 / s

A densidade no insuflador é encontrada a partir da equação e Clapeyron:

ρ 0 = p o R T 0

Lembrando que as temperaturas para esta equação devem estar em kelvin ( K ) , temos que:

ρ 0 = 100 ⋅ 10 3 287 ⋅ 273 + 17

ρ 0 = 1,201   k g / m 3

Passo 2

Por analogia, temos que:

ρ 1 = p 1 R T 1

ρ 1 = 100 ⋅ 10 3 287 ⋅ 273 + 4 7

ρ 1 = 1,09   k g / m 3

E:

ρ 2 = p 2 R T 2

ρ 2 = 100 ⋅ 10 3 287 ⋅ 273 + 97

ρ 2 = 0,942   k g / m 3

A vazão mássica na seção 0 é dada por:

Q m 0 = ρ 0 Q 0

Q m 0 = 1,201 4,5

Q m 0 = 5,41   k g / m 3

Passo 3

Aplicando a condição de Reynolds R e = 10 5 para a seção ( 2 ) temos que:

R e 2 = v 2 D 2 v

v 2 = 10   m / s

A vazão mássica nesta seção é dada por:

Q m 2 = ρ 2 v 2 A 2

Q m 2 = ρ 2 v 2 π D 2 2 4

Q m 2 = 4,73   k g / s

Podemos então encontrar a vazão volumétrica na seção ( 2 ) :

Q 2 = Q m 2 ρ 2

Q 2 = 4,73 0,942

Q 2 = 5,021   m 3 / s

Passo 4

Pela equação da continuidade a vazão mássica é conservada, logo:

Q m 0 = Q m 1 + Q m 2

Portanto:

Q m 1 = 5,41 - 5,021

Q m 1 = 0,68   k g / s

Portanto:

Q 1 = Q m 1 ρ 1

Q 1 = 0,624   m 3 / s

Aplicando a condição de Reynolds, temos que:

R e 1 = v 1 D 1 v

R e 1 = Q 1 D 1 A 1 v

R e 1 = Q 1 D 1 π D 1 2 4 v

Logo:

D 1 = 4 Q 1 π R e v

Substitundo os valores conhecidos, temos que:

D 1 = 4 0,624 π 10 5 8 ⋅ 10 - 5

D 1 = 0,099   m

Resposta

a )   D 1 = 0,099   m

b )   Q 1 = 0,624   m 3 / s

Q 2 = 5,021   m 3 / s

c )   Q m 1 = 0,68   k g / s

Q m 2 = 4,73   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo redondo e poroso, com D = 60m m , transporta água. A velocidade de entrada é uniforme com V 1 = 7,0m / s . A água vaza para fora do tubo através das paredes porosas, radialmente e com simetria
O perfil de velocidade para escoamento laminar em uma seção anular é dado por u r = - ∆ p 4 μ L R 0 2 - r 2 + R 0 2 - R i 2 ln ⁡ R i R 0 ln ⁡ R 0 r em que Δ p / L = - 10k P a / m é o gradiente de pres
Um tanque retangular, usado para fornecer água em uma experiência de número de Reynolds, tem profundidade de 230m m , largura W = 150m m e comprimento L = 230m m . O número de Reynolds da água do tubo
Um acumulador hidráulico é projetado para reduzir as pulsações de pressão do sistema hidráulico de uma máquina operatriz. Para o instante mostrado, determine a taxa à qual o acumulador ganha ou perde
Um tanque de volume fixo contém salmoura com massa específica inicial, ρ i , maior que a da água. Água pura entra no tanque em regime permanente e misturasse perfeitamente com a salmoura. O nível do l