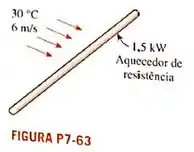
Um fio de resistência elétrica de de comprimento e de potência é feito de de diâmetro de aço inoxidável . O fio de resistência opera em um ambiente a . Determine a temperatura da superfície do fio se for resfriado por um ventilador que sopra ar a uma velocidade de .

Fala galera!!

Para resolver essa questão, podemos começar calculando o Número de Reynolds para o fluxo de ar na superfície do fio. Assim temos:

Aqui, é a velocidade do ar, é o diâmetro do fio e é a viscosidade cinemática do ar. Substituindo os termos da equação acima pelos dados fornecidos, temos:

Agora vamos calcular o Número de Nusselt. Temos que a relação adequada para do número de Nusselt correspondente a esse número de Reynolds para um escoamento cruzado sobre um cilindro é

Substituindo os termos da equação acima pelos dados obtidos, temos:

O Número de Nusselt pode ser escrito usando a seguinte relação:

Usando a relação acima, podemos encontrar o coeficiente de transferência de calor por convecção. Assim temos:

Aqui, é o diâmetro do tubo e é a condutividade térmica do ar.

Agora, podemos calcular a temperatura da superfície usando a lei do resfriamento de Newton. Assim temos:

Aqui, é a área da superfície do tubo , é o coeficiente de transferência de calor por convecção, é a calor transferido para o ar e é a temperatura do ar ambiente. Substituindo os termos da equação acima pelos dados obtidos, temos:

Agora, vamos calcular a temperatura de filme para ver se a suposição feita foi válida.

Se refizermos os cálculos com a temperatura de filme de , vamos encontrar que a temperatura da superfície é:

Propriedades:

Temperatura do filme seja de . Propriedades do ar Tabela A-15:

Condutividade térmica do ar:

Viscosidade cinemática do ar:

Numero de Prandtl:

Número de Reynolds:

Número de Nusselt

Coeficiente de transferência de calor por convecção:

Temperatura da superfície:

Portanto, a temperatura da superfície do fio é .