Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 16
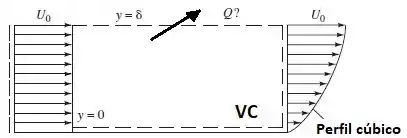
Um fluido incompressível escoa sobre uma placa plana impermeável, como mostra abaixo, com um perfil uniforme na entrada, , e um perfil polinomial cúbico na saída
onde .
Calcule a vazão volumétrica Q através da superfície superior do volume de controle.
Passo 1
E “lerigou” para mais uma questãozinha de mecflu?
Então, vamos lembrar do nosso balanço de massa para um fluido incompressível e, portanto, não tendo acúmulo, em outras palavras, regime permanente.
Olhando para o nosso desenho, você concorda comigo que temos duas vazões que estão saindo, certo? É o “Q” que está apontado pra cima e temos o “Qcub” que está saindo com o perfil cúbico. Entrando temos apenas um “Qe”, beleza?
Passo 2
Bora agora calcular essas vazões aí, beleza?
Passo 3
Logo, temos que:
Resposta
Exercícios de Livros Relacionados
Água entra em um canal largo e plano, de altura 2h, com uma velocidade de 2,5m / s . Na saída do canal, a distribuição de velocidades é dada por u u m á x = 1 - y h 2 á em que y é medido a partir da l
No escoamento incompressível através do dispositivo mostrado, as velocidades podem ser consideradas uniformes em todas as seções de entrada e de saída. As seguintes condições são conhecidas: A 1 = 0,1
Um tanque, com volume de 0,4m 3 , contém ar comprimido. Uma válvula é aberta e o ar escapa com velocidade de 250m / s através de uma abertura de 100m m 2 de área. A temperatura do ar passando pela abe
Água é drenada de um tanque cilíndrico, de 0,3m de diâmetro, através de um orifício no fundo do tanque. No instante em que a profundidade da água é 0,6m , a vazão em massa observada no dreno é 4k g /
Água entra em um canal bidimensional de largura constante, h = 75,5m m , com velocidade uniforme, U . O canal faz uma curva de 90 º º que distorce o escoamento de modo a produzir, na saída, o perfil l