Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 38

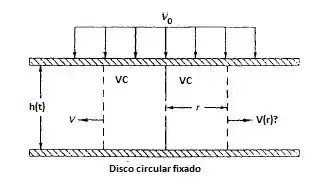
Um fluido incompressível está sendo espremido entre dois grandes discos circulares, pelo movimento de descida uniforme V 0 do disco superior. Considere escoamento radial, unidimensional, para fora, use o volume de controle mostrado para reduzir uma expressão para V r .

Passo 1

E aí meus friends, tudo bem? Esse exercício parece complicado, né? Mas relaxa que vamos fazer ele juntos e você vai ver que é sucesso!!

Vamos lá, se você olhar bem, vai perceber que nos nossos volumes de controle não tem vazão de entrada, apenas vazão de saída e um termo de acúmulo presente, show?

d d t ∫ ρ d v + ∫ ρ V s a í d a d A = 0

Passo 2

Podemos então integrar d v e d A com o volume de VC e a área transversal de escoamento, correto?

d d t ρ v + ρ V s a í d a A

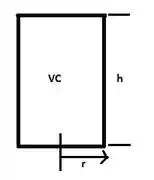
Se você observar comigo, o volume de controle ele será dado pela área da base circular fixada (um disco) pela sua altura h. Enquanto a área de escoamento de saída será dada pelo produto do comprimento do disco e sua altura h.

d d t ρ π r 2 h + ρ 2 π r h V = 0

Passo 3

Vamos agora desenvolver nosso equacionamento. Considerando escoamento incompressível, isso quer dizer que a densidade não varia com o tempo e pode sair da derivada, certo? De igual forma, o raio do nosso disco é constante, ou melhor, o raio dentro do nosso volume de controle é constante e de igual modo poderá sair da integral. E agora, observando a altura, a gente sabe que ela não será constante durante o processo de escoamento, logo.

ρ π r 2 d h d t + ρ π r 2 h V = 0 → r 2 d h d t + 2 r h V = 0

Agora vamos analisar o seguinte, você concorda comigo que h é a distância que o disco superior estará “andando” ao longo do processo, certo? E o que é a variação de distância pelo tempo? VELOCIDADE!!!!!! Mas como estamos no sentido negativo, vamos ter que colocar um sinal negativo, beleza?

d h d t = - V 0

Como resultado, vamos ter:

- r 2 V 0 = - 2 r h V → V = r V 0 2 h

Resposta

V = r V 0 2 h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em sua cozinha, a pia tem 0,6m por 45,7c m e tem 30,5c m de profundidade. Você a está enchendo com água com uma vazão de 252 × 10 - 6m 3 / s . Quanto tempo (em minutos) você leva para encher metade da
Óleo escoa em regime permanente formando uma fina camada em um plano inclinado para baixo. O perfil de velocidade é dado por: Expresse a vazão mássica por unidade de largura em termos de ρ , μ , g , θ
Normas para ventilação de ar em salas de aula especificam uma renovação do ar da sala com uma vazão de pelo menos 8,0L / s de ar fresco por pessoa (estudantes e professor). Um sistema de ventilação pa
Um fluido incompressível escoa em regime permanente por meio de um canal plano divergente. Na seção de entrada, de altura H , o escoamento é uniforme com módulo V 1 . Na saída, de altura 2 H , o perfi
Água entra em um canal largo e plano, de altura 2h, com uma velocidade de 2,5m / s . Na saída do canal, a distribuição de velocidades é dada por u u m á x = 1 - y h 2 á em que y é medido a partir da l