A superfície superior de um forno está a em uma condição de operação particular, quando o ar da sala encontra-se a . Para reduzir a perda de calor do forno e minimizar o perigo de queimaduras, propõe-se criar, com a adição de uma placa de cobertura, um espaço de ar com de espessura.

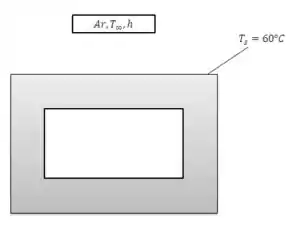
(a) Admitindo a mesma temperatura superficial do forno Ts para ambas as situações, estime a redução na perda de calor por convecção resultante da instalação da placa de cobertura. Qual é a temperatura da placa de cobertura?

Agora que temos as propriedades podemos calcular o número de Rayleigh:

Em que para uma placa horizontal:

Então,

A correlação de Nusselt para uma placa plana com superfície superior aquecida é:

A partir do coeficiente podemos calcular a taxa de transferência de calor por convecção na primeira situação:

Vamos agora determinar qual será a taxa de transferência de calor quando adicionamos a placa de ar. Considerando que não haverá perda ou acúmulo de energia no sistema, a energia transferida do forno para a placa deve ser igual à energia transferida da placa para o ar externo. Então:

Porém, como podemos ver pela equação a taxa de transferência de calor depende da temperatura da interface placa-ar ambiente . Além disso, para obter os coeficientes convectivos também precisaremos desta temperatura.

Para contornar este problema vamos estimar um valor de e usá-lo para encontrar os coeficientes e as taxas de transferência. Se estimarmos um valor próximo do real, devemos verificar que a equação:

Será válida. Caso contrário, teremos valores de taxas diferentes nos dois lados da equação, o que mostra que não estimamos um bom valor para , devendo então estimar um novo valor e repetir o procedimento. Vamos lá?

Vamos estimar que . Então, a temperatura média do ar externo será:

As propriedades do ar nesta temperatura são (Tabela A-4, apêndice A):

O próximo passo será calcular o número de Rayleigh:

A correlação de Nusselt é:

A partir do coeficiente convectivo iremos calcular a taxa de transferência de calor por convecção entre a superfície da placa e o ambiente:

Iremos agora calcular a taxa de transferência de calor através da placa contendo ar. Começamos pela temperatura média do ar contido na placa:

Para esta temperatura as propriedades do ar são (Tabela A-4, apêndice A):

O número de Rayleigh para um espaço confinado entre duas placas paralelas é:

Sendo que desta vez, é a distância entre as placas. Ou seja, .

A correlação para o número de Nusselt em um espaço confinado entre duas placas paralelas é:

Então, a taxa de transferência de calor é:

Como encontramos taxas de transferência de calor similares podemos assumir que:

Para finalizar precisamos calcular qual foi a redução na taxa de transferência de calor após a adição da placa.

Vamos considerar para os cálculos uma média entre os valores de que encontramos para a situação em que a placa é inserida. Ou seja, vamos considerar .

A redução percentual é dada por:

Então, com a adição da placa a perda de energia foi reduzida em .