Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 31

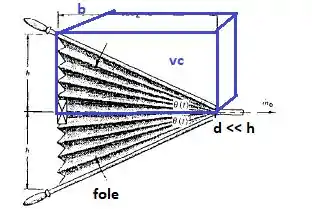
Um fole pode ser modelado como um volume deformável em forma de cunha, como mostra a figura. A válvula de retenção do lado esquerdo (pregueado) fica fechada durante o sopro. Se b é a largura do fole, normal ao papel, deduza uma expressão para o fluxo de massa m ˙ 0 na saída, em função do ângulo do curso durante o sopro, θ t .

Passo 1

E aí, galera!! Tudo bem? Vamos encarar mais esse problema de mecflu?

Para um volume de controle em volta da nossa figura, vamos observar que só há uma vazão de saída e um acúmulo de massa, uma vez que não temos vazão de entrada!!!

d d t v ρ + m ˙ s a i = 0

Onde podemos dizer que o volume v do nosso volume de controle será dado por: v = b h L , já que nosso volume e controle pode ser dado como mostrado abaixo!!

Pela relação trigonométrica podemos escrever tudo em função de θ e L .

t a n θ = h L → h = L t a n θ

v = b h L = b L 2 t a n θ

Passo 2

Considerando que L seja constante, resolvemos o balanço de massa para a vazão de saída, tal que:

d d t v ρ + m ˙ s a i = 0

m ˙ s a i = - d d t ρ b L 2 t a n θ = - ρ b L 2 sec 2 ⁡ θ d θ d t  

Resposta

m ˙ s a i = = - ρ b L 2 sec 2 ⁡ θ d θ d t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha expressões para a vazão volumétrica e para o fluxo de quantidade de movimento através da seção transversal do volume de controle mostrado no diagrama.
A distribuição de velocidades para escoamento laminar em um longo tubo circular de raio R é dada pela expressão unidimensional, V → = u i ^ = u m a x 1 - r R 2 i ^ Para este perfil, obtenha expressões
Um laboratório universitário deseja construir um túnel de vento de vazão 15 m 3 s com velocidades variáveis do ar. Para isso, propõe-se construir o túnel com uma sequência de três seções de teste circ
A área sombreada mostrada está em um escoamento onde o campo de velocidade é dado por V =a x î=b y ĵ î ĵ; a=b=1s - 1 e as coordenadas são medidas em metros. Avalie a vazão volumétrica e o fluxo de qua
Para o escoamento do Problema 4.17, obtenha uma expressão para o fluxo de energia cinética, ∫ ( V 2 2 )ρ V → d A → , através da seção normal ao eixo do tubo.