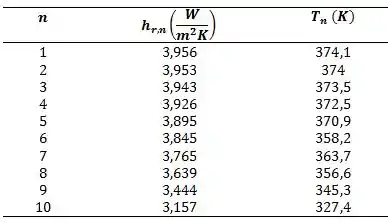
Uma folha metálica delgada, com espessura 0,25 mm e um padrão de orifícios extremamente pequenos, serve como uma grade de aceleração para controlar o potencial elétrico de um feixe de íons. Tal grade é utilizada em um processo de deposição de vapores químicos (chemical vapor deposition – CVD) para a fabricação de semicondutores. A superfície superior da grade está exposta a um fluxo de calor uniforme, causado pela absorção do feixe de íons, . As arestas da folha estão termicamente acopladas a sumidouros de calor que são

resfriados com água e mantidos a 300 K. Nas superfícies superior e inferior da folha há troca de calor por radiação com as paredes da câmara na qual se encontra a folha. Há vácuo no interior desta câmara, cujas paredes são mantidas a 300 K. A condutividade térmica efetiva do

material da folha é de e a sua emissividade é igual a 0,45.

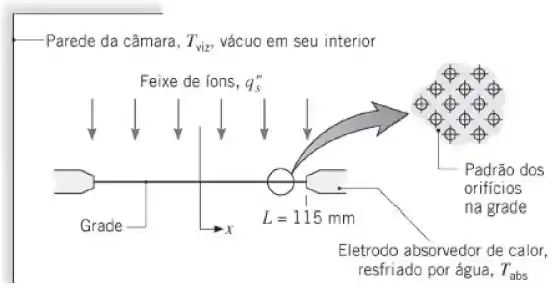
Supondo condução unidimensional e usando um método de diferenças finitas, representando a malha por 10 nós na direção x, estime a distribuição de temperaturas na grade.

Sugestão: Para cada nó necessitando de um balanço de energia, use a forma linearizada da

equação para a taxa radiante, Equação 1.8, com o coeficiente de transferência de calor por radiação hr, Equação 1.9, calculado para cada nó.

Eu seii que vocês estão pegando o gosto ein !!

Bora seguir então !!

O problema nos disse que nós queremos 10 nós na direção x, certo?

Então bora desenhar:

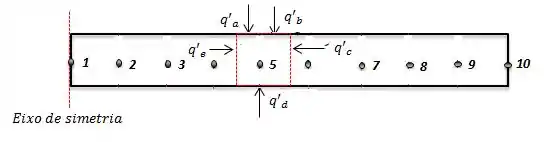
Quando nós analisamos um volume de controle vamos perceber que temos duas formas de calor entrando na parte superior, e , referentes ao feixe de íons e a radiação, na parte inferior nós temos radiação também, , e para finalizar nós temos calor por condução dos pontos adjacentes, e .

Quando fazemos o balanço de energia:

Vamos substituir cada termo para um ponto arbitrário n?

Precisamos da temperatura, certo?

Então vamos isolar:

De acordo com a Equação 1.9, o coeficiente de transferência de calor por radiação hr é dado por:

Nós já sabemos que:

Agora nós substituímos nossos dados nas fórmulas, certo?

Então nós vamos gerar 10 valores para coeficiente radioativo e para a temperatura, certo?

Quando lançamos nossos dados no software obtemos:

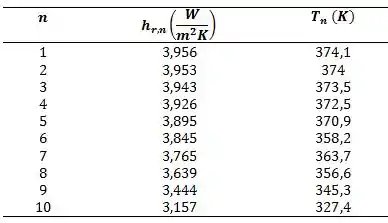
Gostaram desta?