Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 62

Uma análise por diferenças finitas, em condições de regime estacionário, foi efetuada em uma aleta cilíndrica com um diâmetro de 12 mm e condutividade térmica de 15 W m K . O processo de transferência de calor por convecção é caracterizado por uma temperatura no fluido de 25°C e um coeficiente de transferência de calor igual a 25 W m 2 K .

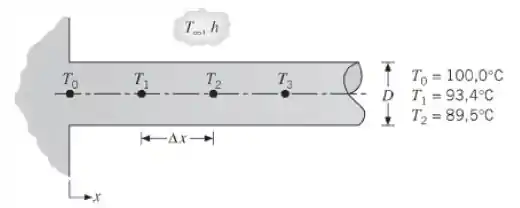
  1. As temperaturas para os três primeiros nós, separados por um incremento espacial de x = 10 mm, são dadas na figura. Determine a taxa de transferência de calor na aleta.
  2. Determine a temperatura no nó 3, T 3 .

Passo 1

Animadíssimos para mais uma?

Então boora lá!!

Desenhando nossos volumes:

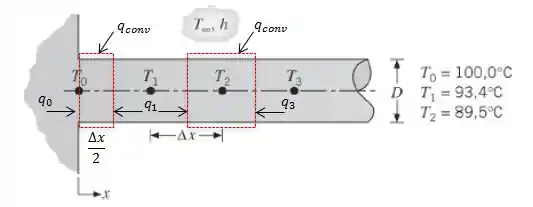
Na letra (a) nós queremos determinar a taxa de transferência de calor na aleta, q 0 , certo?

Para o Ponto 0 nós podemos fazer uma balanço energético:

E e n t r a - E s a i = 0

Analisando a figura nós vemos que existe um calor q 0 entrando, que é o calor que entra na aleta, também temos q 1 e a transferência de calor por convecção, q c o n v :

q 0 + q 1 + q c o n v = 0

Se substituirmos cada termo:

q 1 = k A c T 1 - T 0 ∆ x = π k D 2 T 1 - T 0 4 ∆ x

q c o n v = h P ∆ x 2 T ∞ - T 0 = π h D ∆ x 2 T ∞ - T 0

Substituindo na fórmula e achando q 0 :

q 0 = - π 15 W m K 0,012   m 2 93,4 ° C - 100 ° C 4 0,01   m - π 25 W m 2 K 0,012   m 0,01   m 2 25 ° C - 100 ° C

q 0 = 1,473   W

Agora vamos pra (b)??

Passo 2

Bom turmaa, na letra (b) nós queremos determinar a temperatura no nó 3, T 3 .

Para o Ponto 2 nós podemos fazer uma balanço energético:

E e n t r a - E s a i = 0

Analisando a figura nós vemos que existe um calor q 1 entrando, que é o calor que entra na aleta, também temos q 1 e a transferência de calor por convecção, q c o n v :

q 3 + q 1 + q c o n v = 0

Se substituirmos cada termo:

q 1 = π k D 2 T 1 - T 2 4 ∆ x

q 3 = π k D 2 T 3 - T 2 4 ∆ x

q c o n v = π h D ∆ x 2 T ∞ - T 2

Substituindo na fórmula:

T 3 = - T 1 + 2 T 2 + 4 h ∆ x 2 T ∞ - T 2 k D

E colocando os valores:

T 3 = - 93,4 ° C + 2 ( 89,5 ° C ) - 4 25 W m 2 K 0,01   m 2 25 ° C - 89,5 ° C 15 W m K 0,012   m 2

T 3 = 89,2 ° C

Legal, não foi?

Resposta

  1. q 0 = 1,473   W ;
  2. T 3 = 89,2 ° C .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo elétrico, que experimenta uma geração volumétrica de calor a uma taxa uniforme q , encontra-se semienterrado em um material isolante, enquanto a sua superfície superior está exposta a um proce
Um bastão de tantálio, com 3m m de diâmetro e comprimento de 120m m , é sustentado por dois eletrodos no interior de um grande recipiente onde há vácuo. Inicialmente, o bastão está em equilíbrio com o
Placas de circuito impresso são empilhadas e tratadas pelo aquecimento sob alta pressão, como ilustrado no Problema 5.45 e descrito posteriormente no Problema 5.46. Busca-se uma solução pelo método de
Um bastão de sustentação ( k = 15W / ( m · K ) , α = 4,0 × 10 - 6m 2 / s ), com diâmetro D = 15m m e comprimento L = 100m m , atravessa um canal cujas paredes são mantidas a uma temperatura de T b = 3
Considere o sistema do Problema 4.92. Inicialmente, sem o escoamento dos gases de exaustão, as paredes ( α=5,5×10 - 7m 2 / s ) se encontram a uma temperatura uniforme de 25 ° C . Usando o método implí