Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 63

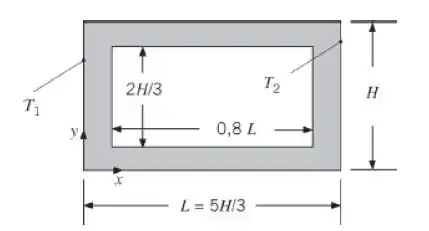
Seja o domínio bidimensional mostrado. Todas as superfícies estão isoladas a menos das superfícies isotérmicas em x = 0 e L.

  1. Use uma análise unidimensional para estimar o fator de forma S.
  2. Estime o fator de forma usando uma análise de diferenças finitas com Δ x   =   Δ y   =   0,05   L . Compare sua resposta com a da parte (a) e explique a diferença entre as duas soluções.

Passo 1

Vamos continuando?

Então galera, na letra (a) nós precisamos estimar o fator forma S assumindo que a condução é unidimensional.

Para estimar essa condução nós vamos pensar assim, o calor vai percorrer uma distância L na direção x, certo?

E na y?

Se esse “buraco” na figura representa 2 H 3 resta para o calor percorrer em y apenas uma distância de H 3 , correto?

Se é assim:

q ' = S k T 1 - T 2 = d y d x k T 1 - T 2

Substituindo:

q ' = H 3 L k T 1 - T 2 = H 3 L k T 1 - T 2

Da figura nós concluímos que:

H 3 L = 1 5

Portanto:

q ' = 1 5 k T 1 - T 2

E o nosso fator forma será:

S = 1 5 = 0,20  

A letra (a) foi de boas, não é?

Passo 2

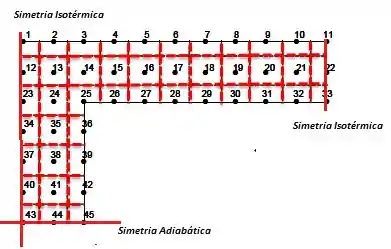
Quando x = 0 e x = L 2 , teremos linhas simétricas isotérmicas e na metade da altura, linha de simetria adiabática. E para finalizar o desenho faremos Δ x   =   Δ y   =   0,05   L :

Se é assim vamos assumir que:

x = 0     →     T 1 = 1

x = L 2     →     T 2 = 1 2

Portanto:

T 1 = T 12 = T 23 = T 34 = T 37 = T 40 = T 43 = T 1 = 1

T 11 = T 22 = T 33 = T 2 = 0,5

Os demais pontos são internos!

Ponto 2:

T 1 + T 3 + 2 T 1 3 - 4 T 2 = 0

Ponto 3:

T 2 + T 4 + 2 T 1 4 - 4 T 3 = 0

Ponto 4:

T 3 + T 5 + 2 T 1 5 - 4 T 4 = 0

Ponto 5:

T 4 + T 6 + 2 T 1 6 - 4 T 5 = 0

Ponto 6:

T 5 + T 7 + 2 T 1 7 - 4 T 6 = 0

Ponto 7:

T 6 + T 8 + 2 T 18 - 4 T 7 = 0

Ponto 8:

T 7 + T 9 + 2 T 19 - 4 T 8 = 0

Ponto 9:

T 8 + T 10 + 2 T 20 - 4 T 9   =   0

Ponto 10:

T 9 + T 11 + 2 T 21 - 4 T 10   =   0

Ponto 13:

T 12 + T 2 + T 14 + T 24 - 4 T 13   =   0

Ponto 14:

T 13 + T 3 + T 15 + T 25 - 4 T 14   =   0

Ponto 15:

T 14 + T 4 + T 16 + T 26 - 4 T 15   =   0

Ponto 16:

T 15 + T 5 + T 17 + T 27 - 4 T 16   =   0

Ponto 17:

T 16 + T 6 + T 18 + T 28 - 4 T 17   =   0

Ponto 18:

T 17 + T 7 + T 19 + T 29 - 4 T 18   =   0

Ponto 19:

T 18 + T 8 + T 20 + T 30 - 4 T 19   =   0

Ponto 20:

T 19 + T 9 + T 21 + T 31 - 4 T 20   =   0

Ponto 21:

T 20 + T 10 + T 22 + T 32 - 4 T 21   =   0

Ponto 24:

T 2 3 + T 1 3 + T 2 5 + T 3 5 - 4 T 2 4   =   0

Ponto 25:

2 T 2 4 + 2 T 1 4 + T 2 6 + T 3 6 - 4 T 2 5   =   0

Ponto 26:

T 2 5 + 2 T 1 5 + T 2 7 - 4 T 2 6   =   0

Ponto 27:

T 2 6 + 2 T 1 6 + T 3 8 - 4 T 2 7   =   0

Ponto 28:

T 2 7 + 2 T 1 7 + T 2 9 - 4 T 2 8   =   0

Ponto 29:

T 2 8 + 2 T 1 8 + T 30 - 4 T 2 9   =   0

Ponto 30:

T 2 9 + 2 T 1 9 + T 31 - 4 T 30   =   0

Ponto 31:

T 3 0 + 2 T 20 + T 32 - 4 T 31   =   0

Ponto 32:

T 3 1 + 2 T 2 1 + T 3 3 - 4 T 32   =   0

Ponto 35:

T 3 4 + T 24 + T 36 + T 3 8 - 4 T 35   =   0

Ponto 36:

2 T 35 + T 25 + T 39 - 4 T 36   =   0

Ponto 38:

T 3 7 + T 35 + T 3 9 + T 41 - 4 T 3 8   =   0

Ponto 39:

2 T 3 8 + T 36 + T 42 - 4 T 3 9   =   0

Ponto 41:

T 4 0 + T 38 + T 42 + T 44 - 4 T 41   =   0

Ponto 42:

2 T 41 + T 3 9 + T 4 5 - 4 T 42   =   0

Ponto 44:

T 4 3 + 2 T 41 + T 4 5 - 4 T 44   =   0

Ponto 45:

T 44 + T 42 - 2 T 45   =   0

Passo 3

Quando nós assumimos que k = 1 W m K e h = 1 , nós podemos lançar nossos dados no software IHT e achar as temperaturas:

Beleza !! Nós achamos as temperaturas, mas não é bem isso que queríamos, certo?

Queremos o fator de forma S, e para isso vamos achar o calor!

Como a troca de calor vai ocorrer entre os ponto 11 e 10, 21 e 22 e 32 e 33

q '   = T 10   - T 1 1 k d x d y 2   +   T 21   - T 22 k . d y d x   +   T 32   - T 32 k d x d y 2

Substituindo nossos dados:

q ' = 0,1074

E quando lembramos da fórmula do Passo 1:

q ' = S k T 1 - T 2

Substituindo novamente:

S = 0,2147

Legal, não foi?

Resposta

  1. S = 1 5 = 0,20   ;
  2. S = 0,2147 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema comum para o aquecimento de uma grande área superficial consiste em passar ar quente através de dutos retangulares localizados abaixo da superfície. Os dutos são quadrados e posicionados na
Seja o Problema 4.69. Um engenheiro deseja medir a temperatura superficial do fino revestimento, pintando ele de preto (ε = 0,98) e usando um dispositivo de medição infravermelho para, de forma não in
Um longo cilindro sólido, com diâmetro D = 25 mm, é formado por um núcleo isolante que é coberto por um revestimento metálico altamente polido e muito fino (t = 50 μm), com condutividade térmica de k=
Determine a distribuição de temperaturas em t=30m i n para as condições do Problema 5.116 .(a) Use uma técnica de diferenças finitas explícita, com um incremento de tempo de 600s e um incremento no es
Seja o elemento combustível do Exemplo 5.11 . Inicialmente, o elemento está a uma temperatura uniforme de 250 ° C sem geração de energia. Subitamente, o elemento é inserido no núcleo do reator passand