Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 9

Na instalação, a vazão de 100 L/s divide-se igualmente nos dois ramais. Qual é o momento em relação ao eixo z devido somente à ação da água? Dados: A 2 = A 3 = 2 ⋅ 10 - 3   m 2 ; p 1 = 100   P a ; γ = 10 4   N / m 3

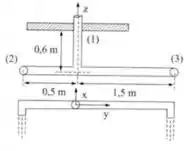
Passo 1

Vamos aplicar a equação 10.28

M z = ∂ ∂ t ∫ V C ρ r 0 v θ d V + ∫ S C ρ r 0 v θ ( v → × n → ) d A

Consideramos que este seja um regime permanente, então a derivada do VC é zero:

∂ ∂ t ∫ V C ρ r 0 v θ d V = 0

Aplicando na equação:

M z = ∫ S C ρ r 0 v θ ( v → × n → ) d A

A velocidade é sempre ortogonal à área, então o produto vetorial é:

v → × n → = v θ

M z = ∫ S C ρ r 0 v θ v θ d A

M z = ∫ S C ρ r 0 v θ d Q

Resolvendo a integral entre os pontos (2) e (3)

M z = ρ 3 r 3 v 3 ⋅ Q 3 - ρ 2 r 2 v 2 Q 2

Passo 2

Vamos fazer algumas considerações:

Primeiro, como a água é um fluido incompressível:

ρ 3 = ρ 2 = ρ

Segundo, como as áreas de saída são iguais, vamos assumir que a vazão por elas é a mesma. Dessa forma, a vazão que entre em (1) é dividida igualmente para (2) e (3).

Q 3 = Q 2 = Q

Q = Q 1 2 = 50 L s = 50 ⋅ 10 - 3 m 3 s

Por consequência, a velocidade de saída em (2) e (3) é a mesma, e pode ser calculada por:

v 2 = v 3 = v

v = Q A = 50 ⋅ 10 - 3   m 3 / s 2 ⋅ 10 - 3   m 2 = 25 m s

Passo 3

Aplicando todas essas considerações na equação:

M z = ρ r 3 v ⋅ Q - ρ r 2 v Q

M z = ρ v Q ( r 3 - r 2 )

Aplicando os valores:

M z = 1000 k g m 3 ⋅ 25 m s ⋅ 50 ⋅ 10 - 3 m 3 s ( 1,5 - 0,5 )

M z = 1250   N m

Resposta

M z = 1250   N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque aberto da Figura P 3.14 contém água a 20 ° C e está sendo enchido através da seção 1 . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação
Uma sala contém poeira com concentração uniforme ,C = ρ p o e i r a ρ . Ela deve ser limpa, insuflando ar novo com uma velocidade V e através de um duto de área A e em uma parede e fazendo a exaustão
A seringa hipodérmica abaixo contém um soro líquido (d = 1,05). Se o soro deve ser injetado em regime permanente a 6 cm³/s, qual deverá ser a velocidade de avanço do êmbolo em cm/s (a) se a fuga na fo
Óleo (d = 0,89) entra na seção 1 da figura abaixo com uma vazão em peso de 250 N/h para lubrificar um mancal de escora. O escoamento permanente de óleo sai radialmente através da folga estreita entre
Um fluido incompressível escoa sobre uma placa plana impermeável, como mostra abaixo, com um perfil uniforme na entrada, u = U o , e um perfil polinomial cúbico na saída u ≈ U o 3 η - η 3 2 onde η = y