Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 53
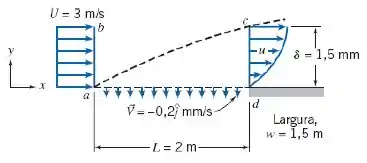
Considere um escoamento incompressível e permanente de ar padrão em uma camada limite sobre toda a extensão da superfície porosa mostrada. Considere também que a camada limite na extremidade a jusante da superfície tenha um perfil de velocidade aproximadamente parabólico dado por
Uma sucção uniforme é aplicada ao longo da superfície porosa, como mostrado. Calcule a vazão volumétrica por meio da superfície , da superfície porosa de sucção e da superfície .
Passo 1
A figura mostra que a ar padrão em uma camada limite sobre toda a extensão da superfície porosa. Podemos aplicar a equação da continuidade no volume de controle desenhado. Assim temos:
Aqui, é a densidade, é a velocidade, é o diferencial de volume e é o diferencial de área.
Nos foi dado que o escoamento é incompressível e permanente. Então a equação se reduz a:
Para fluxo incompressível, o volume da taxa em um volume de controle fixo deve ser igual à taxa de fluxo de volume fora do volume de controle.
Passo 2
Podemos calcular a taxa de fluxo de volume na superfície da seguinte forma:
Substituindo pelos valores conhecidos temos:
Largura da placa: .
A espessura da camada limite: .
Velocidade: .
Substitua os valores na equação acima.
Portanto, a vazão do volume na superfície é .
Passo 3
Podemos calcular a vazão através da superfície porosa da seguinte maneira:
Aqui temos:
Velocidade:
Largura da placa:
Comprimento da placa:
Passo 4
Podemos calcular a vazão através da superfície da seguinte maneira:
Aqui temos:
Velocidade:
Largura da placa:
Altura da placa:
Passo 5
Podemos calcular a vazão através da superfície pela seguinte equação:
Substitua os valores conhecidos na relação acima.
Portanto, a vazão do volume através da superfície é para cima (ou na direção oposta ao volume de controle).