Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 37

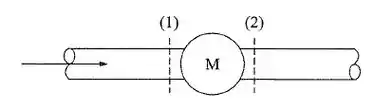
Na máquina da figura, são dados: v 1 = 4   m / s ; A 1 = 0,52   m 2 ; A 2 = 0,4   m 2 ; p 1 = p 2 = 0,1   M P a . O escoamento é isotérmico, a potência fornecida ao fluido compressível pela máquina é 10 kW e o fluxo de calor perdido para o exterior é 0,98 kW. Qual é a vazão em massa através da máquina?

Passo 1

Como o escoamento é isotérmico, temos a seguinte relação entre pressão e densidade do escoamento:

p 2 ρ 2 = p 1 ρ 1 → ρ 1 ρ 2 = p 1 p 2

Nesse exercício, como p 1 = p 2 então ρ 1 = ρ 2 . Nesse caso, a vazão mássica é constante, então podemos escrever:

ρ 1 v 1 A 1 = ρ 2 v 2 A 2 → v 2 = v 1 A 1 A 2 = 4 0,52 0,4 → v 2 = 5,2   m / s

Passo 2

A potência da máquina pode ser escrita como:

N = Q m H M g → H M = N Q m g

Onde Q m é a vazão mássica de ar e g é a aceleração da gravidade. Da mesma forma, o fluxo de calor perdido para o exterior pode ser escrito como:

Q ˙ p e r d i d o = Q m q g → q = Q ˙ p e r d i d o Q m g

Onde q é a variação da energia cinética do escoamento.

Passo 3

Agora podemos aplicar o equilíbrio de cargas para o sistema:

H 1 + q + H M = H 2

v 1 2 2 g + p 1 ρ 1 g + z 1 + q + H M = v 2 2 2 g + p 2 ρ 2 g + z 2

Os pontos 1 e 2 estão no mesmo nível, então z 1 = z 2 , além disso, como p 1 = p 2 e ρ 1 = ρ 2 então os termos contendo a pressão se anulam, de forma que:

v 1 2 2 g + q + H M = v 2 2 2 g

Agora, substituindo os valores conhecidos, temos:

4 2 2 10 + Q ˙ p e r d i d o Q m g + N Q m g = 5,2 2 2 10 → Q ˙ p e r d i d o + N Q m g = 0,552

Q m = Q ˙ p e r d i d o + N 0,552 g = - 980 + 10000 0,552 ( 10 ) → Q m = 1634,1   k g / s

Resposta

Q m = 1634,1   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na extremidade de uma tubulação de diâmetro D , acha-se instalado um bocal que lança um jato de água na atmosfera com diâmetro de 2c m . O manômetro metálico registra uma pressão de 20k P a e a água s
Sabendo que a potência da bomba é 3k W , seu rendimento 75 % e que o escoamento é de 1 para 2 , determinar:A vazão;A carga manométrica da bomba;A pressão do gás.Dados: H p 1,2 = H 5,6 = 1,5m ; H p 3,4
Quais são as vazões de óleo em massa e em peso no tubo convergente da figura, para elevar uma coluna de 20c m de óleo no ponto ( 0 ) ?Dados: desprezar as perdas; γ ó l e o = 8000N / m 3 ó ; g = 10m /
Na instalação da figura, a carga total na seção 2 é 12m . Nessa seção, existe um piezômetro que indica 5m . Dados: γ H 2 O = 10 4N / m 3 ; γ H g = 1,36 × 10 5N / m 3 ; h = 1m ; D 1 = 6c m ; D 2 = 5c m
Um dos métodos para se produzir vácuo numa câmara é descarregar água por um tubo convergente-divergente, como é mostrado na figura. Qual deve ser a vazão em massa de água pelo convergente-divergente,