Uma janela de vidro duplo, vertical, que tem de lado e um espaço de preenchido com ar atmosférico, separa o ar quiescente de uma sala a do ar ambiente externo, também quiescente, a . As trocas radiantes entre as lâminas de vidro, assim como entre as lâminas de vidro e os seus ambientes adjacentes, podem ser desprezadas.

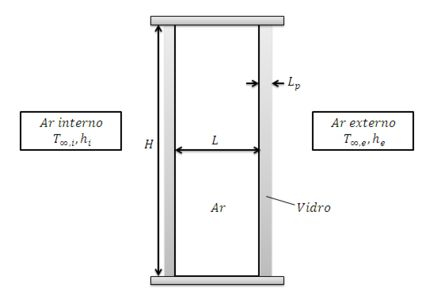
(a) Desprezando a resistência térmica associada à transferência de calor por condução através de cada lâmina de vidro, determine a temperatura correspondente de cada lâmina e a taxa de transferência de calor através da janela.

(b) Comente sobre a validade de se desprezar a resistência condutiva nas lâminas de vidro, se cada uma tiver uma espessura de .

Vamos começar dizendo que e . A temperatura média no ambiente interno será:

As propriedades do ar nesta temperatura são (Tabela A-4, apêndice A):

A partir das propriedades vamos calcular o coeficiente convectivo do ambiente interno. Para isso, o nosso próximo passo será obter o número de Rayleigh:

Vamos agora aplicar a correlação de Nusselt para escoamento sobre placa plana:

Para finalizar o fluxo de calor por convecção natural é:

Vamos calcular os demais fluxos e verificar se encontramos valores próximos a esse. Se encontrarmos significa que nossas estimativas de temperaturas superficiais é próxima ao real.

Nosso próximo passo é calcular o coeficiente convectivo externo. Para isso, começamos calculando a temperatura média do ar no ambiente externo:

As propriedades do ar serão (Tabela A-4, apêndice A):

Com as propriedades podemos calcular o número de Rayleigh:

Vamos agora aplicar a correlação de Nusselt para escoamento sobre placa plana:

Para finalizar o fluxo de calor por convecção natural é:

Como podemos ver, chegamos em um valor próximo ao que calculamos para o ambiente interno. O último passo para garantir que estimamos um bom valor para as temperaturas superficiais será obter o fluxo de calor no espaçamento da janela.

Assim como nos passos anteriores começaremos calculando a temperatura média no espaçamento. Ela é dada por:

De acordo com a tabela A-4 do apêndice A, para esta temperatura:

O próximo passo é calcular o número de Rayleigh para o ambiente entre as janelas:

A correlação para o número de Nusselt em ambientes confinados é:

E o fluxo de transferência de calor por convecção é:

Logo, como encontramos três valores de fluxo que são bem próximos podemos dizer que as temperaturas superficiais das placas são:

Vamos agora para o item (b). Neste item devemos verificar se a resistência condutiva poderia ser desprezada.

Para isso, iremos começar usando os valores dos coeficientes convectivos do item (a) para calcular as resistências convectivas. A resistência térmica de convecção é dada por:

Então:

Agora que temos ideia da ordem de grandeza das resistências convectivas vamos verificar qual é a resistência condutiva. O primeiro passo é obter a condutividade térmica do vidro. Pela tabela A-3 do apêndice A, .

A resistência condutiva é:

Como podemos a resistência condutiva possui um valor bem inferior ao das resistências de convecção. Então, é razoável a consideração de que podemos desprezar a resistência condutiva nos cálculos.