Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 19
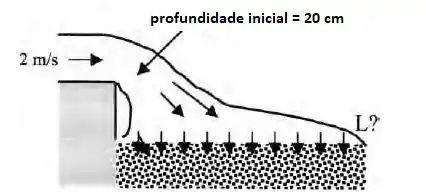
Água de uma drenagem pluvial escoa para uma saída sobre um leito poroso que absorve a água a uma velocidade vertical uniforme de 8 mm/s, como mostra abaixo. O sistema tem 5 m de largura normal ao papel. Encontre o comprimento L do leito que absorverá completamente a água da chuva.
Passo 1
Essas questões com aplicações assim são muito legais de serem feitas, galera! E você vai ver que não tem nada de um bicho de sete-cabeças nisso!!!
Além disso, vou te mostrar que o tamanho da continha que você terá que fazer e, afinal, esse tipo de projeto pode evitar alagamentos em diversos locais :D
LERIGOU COMIGO!
Para que todo o leito absorve a água completamente, a vazão de água de entrada no meio poroso deve ser igual a vazão de saída também, certo?
Passo 2
A área de escoamento tem 20 cm de profundidade e 5 m de largura. Quando o exercício aqui diz que tem 5 m de comprimento no sentido normal ao papel, ele quer dizer que a largura está crescendo na sua direção!!! Simmmm, você faz parte dessa questão, olha que massa!!!!