Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 16

Um líquido incompressível com viscosidade desprezível e massa específica ρ = 850 kg/m3 escoa em regime permanente através de um tubo horizontal. A área da seção transversal do tubo varia linearmente de 100 cm2 para 25 cm2 ao longo de um comprimento de 2 m. Desenvolva uma expressão e trace o gráfico para o gradiente de pressão e para a pressão em função da posição ao longo do tubo, se a velocidade da linha de centro na entrada é 1 m/s e a pressão na entrada é 250 kPa. Qual é a pressão na saída? Sugestão: Use a relação:

u ∂ u ∂ x = 1 2 ∂ d x ( u 2 )

Passo 1

Pessoal, este é um problema de escoamento unidirecional que pede a aceleração e gradiente de pressão. Para começar, vamos aplicar a equação da aceleração 5.11a:

a x = D u D t = u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z + ∂ u ∂ t

Assumindo que:

  1. regime permanente
  2. fluido incompressível
  3. fluxo uniforme pela seção
  4. g x = 0
  5. Velocidades de escoamento em y e em z são nulas.

A equação simplifica para:

a x = u ∂ u ∂ x

Passo 2

A equação do da vazão é dada por:

Q = V ∙ A

A velocidade do fluido na entrada é dada u 1 , então podemos escrever a vazão como:

Q = u 1 ∙ A 1

O enunciado fala que a área do tubo varia linearmente de 100cm² para 25cm² ao longo de 2 metros. Veja o desenho representando:

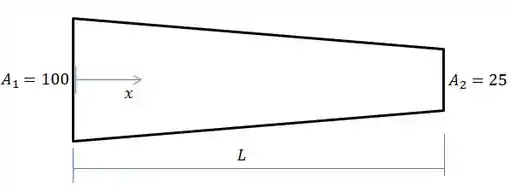
Podemos escrever matematicamente a área em função da distância x:

A = A 1 - A 1 - A 2 L x

A vazão pode ser representada na forma geral por:

Q = u x ∙ A

Relacionando esta equação da vazão com a da entrada, temos:

Q = u 1 ∙ A 1 =   u x ∙ A

u x = u 1 A 1 A

Substituindo o valore de A:

u x = u 1 A 1 A 1 - A 1 - A 2 L x

Passo 3

No passo 1 encontramos a expressão da aceleração.

a x = u ∂ u ∂ x

Substituindo o valor de u encontrado no passo 2:

a x = u 1 A 1 A 1 - A 1 - A 2 L x ∂ u 1 A 1 A 1 - A 1 - A 2 L x ∂ x

Vamos trabalhar na derivada:

∂ u 1 A 1 A 1 - A 1 - A 2 L x ∂ x = u 1 A 1 ∂ 1 A 1 - A 1 - A 2 L x ∂ x

u 1 A 1 ∂ 1 A 1 - A 1 - A 2 L x ∂ x = u 1 A 1 ∂ A 1 - A 1 - A 2 L x - 1 ∂ x

Vamos fazer a substituição:

t = A 1 - A 1 - A 2 L x

d t = A 2 - A 1 L d x

Então:

d A 1 - A 1 - A 2 L x - 1 d x = d t - 1 L A 2 - A 1 d t = A 2 - A 1 L d t - 1 d t

= A 2 - A 1 L - 1 t 2

Voltando com os valores originais:

A 2 - A 1 L - 1 t 2 = A 2 - A 1 L 1 A 1 - A 1 - A 2 L x 2

= A 2 - A 1 L L 2 L A 1 - A 1 - A 2 x 2

= L A 2 - A 1 L A 1 - ( A 1 - A 2 ) x 2

Jogando na expressão toda:

a x = u 1 A 1 A 1 - A 1 - A 2 L x u 1 A 1 L A 2 - A 1 L A 1 - A 1 - A 2 x 2

a x = u 1 L A 1 L A 1 - A 1 - A 2 x u 1 A 1 L A 2 - A 1 L A 1 - A 1 - A 2 x 2

a x = u 1 2 A 1 2 L 2 A 2 - A 1 L A 1 - A 1 - A 2 x 3

Passo 4

Para encontrar o gradiente de pressão vamos usar a equação de Euler 6.2a do livro:

ρ u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z + ∂ u ∂ t = ρ g x - ∂ p ∂ x

Pela equação da aceleração do Passo 1, podemos simplificar a expressão acima:

ρ a x = ρ g x - ∂ p ∂ x

ρ a x = - ∂ p ∂ x

O gradiente de pressão é dado então por:

∂ p ∂ x = - ρ u 1 2 A 1 2 L 2 A 2 - A 1 L A 1 - A 1 - A 2 x 3

Sabendo que:

ρ = 850 k g m 3 ;     u 1 = 1 m s ;         p 0 = 250   k P a ;       A 1 = 100   c m 2 ;       A 2 = 25   c m 2

∂ p ∂ x = 850 1000 1 2 100 2 2 2 100 - 25 2 100 - 100 - 25 x 3

∂ p ∂ x = 2550000   2 00 - 75 x 3

Passo 5

O diferencial total da pressão é dado pela expressão:

d p = ∂ p ∂ x d x

Combinando as equações, temos:

d p = - ρ a x d x

Substituindo a x :

d p = - ρ u 1 2 A 1 2 L 2 A 2 - A 1 L A 1 - A 1 - A 2 x 3 d x

Para encontrar a pressão, basta integrar a função acima. Entretanto, será uma integral muito complexa. Agora é o momento perfeito para usar a dica do enunciado:

u ∂ u ∂ x = 1 2 ∂ d x ( u 2 )

No passo 3, encontramos que:

a x = u ∂ u ∂ x

Então:

a x = u ∂ u ∂ x = 1 2 ∂ d x ( u 2 )

Substituindo na equação da pressão:

d p = - ρ 1 2 ∂ d x ( u 2 ) d x

Integrando a expressão:

p ( x ) - p 0 = - ρ 2 ∫ 0 x u 2 d x = - ρ 2 u x 2 - u 1

p x = p 0 - ρ 2 u x 2 - u 1 2

Substituindo u x   e   u 1 , ficamos com:

p x = p 0 - ρ 2 u 1 A 1 A 1 - A 1 - A 2 L x 2 - u 1 2

p x = p 0 - ρ u 1 2 2 A 1 A 1 - A 1 - A 2 L x 2 - 1

Passo 6

A pressão na saída vai ser quando x=L. Usando os dados do enunciado:

ρ = 850 k g m 3 ;     u 1 = 1 m s ;         p 0 = 250   k P a ;       A 1 = 100   c m 2 ;       A 2 = 25   c m 2

p 2 = 250 - 850 1000 ( 1 2 ) 2 100 100 - 100 - 25 2 2 2 - 1

p 2 = 243,625   k P a

Resposta

∂ p ∂ x = - ρ u 1 2 A 1 2 L 2 A 2 - A 1 L A 1 - A 1 - A 2 x 3

p x = p 0 - ρ u 1 2 2 A 1 A 1 - A 1 - A 2 L x 2 - 1

p 2 = 243,625   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.2 Um campo de escoamento incompressível e sem atrito é dado por V → = A x + B y i ^ + B x - A y j ^ , em que A = 2 s - 1 , B = 2 s - 1 e as coordenadas são medidas em metros. Determine o módulo e o
6.7 Considere o campo de escoamento dado por V → = A xs e n2 π ω t i ^ + A ys e n2 π ω t j ^ , em que A = 2s - 1 e ω = 1s - 1 . A massa específica do fluido é 2 kg/m³. Encontre expressões para a acele
Em um escoamento bidimensional sem atrito e incompressível (ρ = 1500 kg/m3), o campo de velocidade em m/s é dado por V → = A x + B y i ^ + B x - A y j ^ , as coordenadas são medidas em metros, e A = 4
O campo de velocidade para um dipolo plano é dado na Tabela 6.2. Determine uma expressão para o gradiente de pressão em qualquer ponto ( r ,θ ).
Um “chip” retangular de microcircuito flutua sobre uma fina camada de ar, com espessura h = 0,5 mm, acima de uma superfície porosa. A largura do chip é b = 40 mm, conforme mostrado. O seu comprimento,