Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 26
A componente x da velocidade em um campo de escoamento incompressível, bidimensional é dada por , em que v é em m/s, as coordenadas são medidas em metros e Não há componente ou variação de velocidade na direção z. Calcule a aceleração de uma partícula fluida no ponto (x, y) = (1, 2). Estime o raio de curvatura da linha de corrente que passa por este ponto. Trace a linha de corrente e mostre os vetores velocidade e aceleração no gráfico. (Considere a forma mais simples da componente da velocidade em x.)
Passo 1
Pessoal, temos um escoamento em 2D e incompressível, além do campo de velocidade. Então, vamos usar a equação 5.3 do livro, que aborda a equação da continuidade para estas condições:
Onde:
Substituindo os valores, temos:
A velocidade em x (u), pode ser encontrada pela expressão:
Substituindo e integrando, temos:
Onde f(y) é uma função apenas de y, isto é, ela é como se fosse a constante da integral. Como o enunciado não cita nada sobre esta função, vamos escolher a mais simples:
Podemos então escrever a expressão do campo de velocidade:
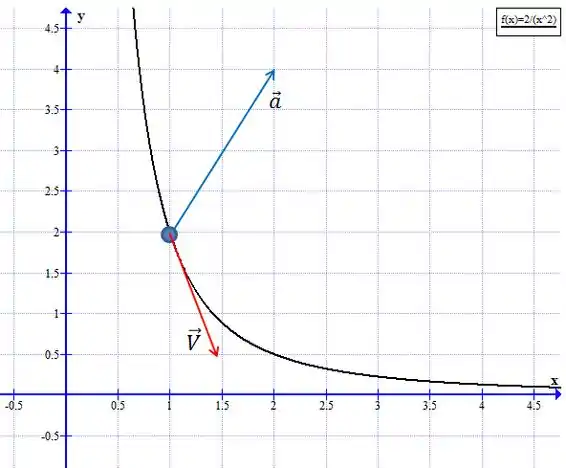
No ponto (1,2), o vetor velocidade vale:
Passo 2
A equação da aceleração da partícula é dada pela equação:
Podemos simplificar a expressão, pois não há componente de velocidade em z vamos considerar que não há aceleração local. Ficamos então com:
Substituindo os valores, temos:
No ponto (1,2), o vetor aceleração vale:
Passo 3
Para encontrar o raio de curvatura da linha de corrente, vamos usar o conceito da aceleração normal:
Onde é o vetor unitário normal. Para encontra-lo, vamos usar o conceito do vetor tangencial, uma vez que eles são perpendiculares. Temos então:
O vetor unitário tangencial possui mesma direção do vetor velocidade. Portanto, usamos a expressão:
Substituindo, temos:
Voltando para a equação da aceleração normal:
Passo 4
A inclinação da linha de corrente é dada por:
Temos então a expressão:
Integrando, temos:
Aplicando a exponencial, temos:
No ponto (1,2), temos:
Esboçando um gráfico, ficamos com:
