Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 37
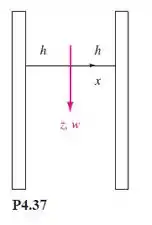
Um líquido viscoso de constantes cai por causa da gravidade entre duas placas separadas por uma distância 2h, como na Figura P4.37. O escoamento é totalmente desenvolvido, com um único componente de velocidade . Não há gradientes de pressão aplicados, somente a gravidade. Resolva a equação de Navier-Stokes para o perfil de velocidade entre as placas.
Passo 1
Bora bora pra mais uma!
Só temos movimento em uma direção ai, em z né, então bora aplicar Navier-Stokes em z, assim:
Considerando ou seja, um não deslizamento, teremos que:
A solução para tal é dada por:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A componente de velocidade na direção da corrente da camada limite sobre placa plana permanente, incompressível, laminar e com espessura δ é aproximada pelo perfil de onda senoidal do Problema 10 - 85
A componente da velocidade na corrente de uma camada limite sobre placa plana permanente, incompressível, laminar e de espessura d é aproximada pela expressão linear simples, u = U y / δ para yδ e u =
Normalmente pensamos nas camadas limite como se elas estivessem ocorrendo ao longo de paredes sólidas. No entanto, há outras situações de escoamento nas quais a aproximaçãoda camada limite também é ap
Neste capítulo, afirmamos que a aproximação de camada limite estabelece uma “ponte” entre a equação de Euler e a equação de Navier-Stokes. Explique.
Considere uma região irrotacional de escoamento planar no plano r θ . Mostre que a função de corrente ψ satisfaz a equação de Laplace em coordenadas cilíndricas.