Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 142

Em um evento de erupção do vulcão, a lava encontrada fluindo no chão tem temperatura de 1200°C. O chão estava inicialmente a 15°C e o fluxo de lava possui um coeficiente de transferência de calor por convecção de 3500 W m 2 K . Determine (a) a temperatura da superfície do solo e (b) fluxo de calor após 2 s de fluxo de lava. Suponha que o terreno tenha propriedades de solo seco.

Passo 1

Bora continuar ??

Para calcular a temperatura da superfície do solo nós podemos usar a equação:

T s - T i T ∞ - T i = e r f c   x 2 α t - e h ² α t k ² e r f c   h α t k

Nós sabemos que:

α = k ρ c p

Substituindo:

T s - T i T ∞ - T i = e r f c   x 2 k t ρ c p - e h ² t k ρ c p e r f c   h k t ρ c p k

Agora nós precisamos ver quais dados temos e quais não, ok?

T ∞ = 1200 ° C

T i = 15 ° C

h = 3500 W m 2 K

t = 2 s

Como estamos na superfície:

x = 0   m

E tabelado para o solo nós temos:

k = 1 W m K

ρ = 1500 k g m 3

c p = 1900 J k g K

Agora é só substituir:

T s - 15 ° C 1200 ° C - 15 ° C = e r f c   0   m 2 1 W m K 2 s 1500 k g m 3 1900 J k g K - e 3500 W m 2 K 2 2 s 1900 J k g K 1500 k g m 3 e r f c   3500 W m 2 K 1 W m K 2 s 1500 k g m 3 1900 J k g K 1 W m K

T s - 15 ° C 1200 ° C - 15 ° C = e r f c   0 - e 8,596 e r f c   2,932

Passo 2

Para a função erfc nós precisamos dessa tabelinha:

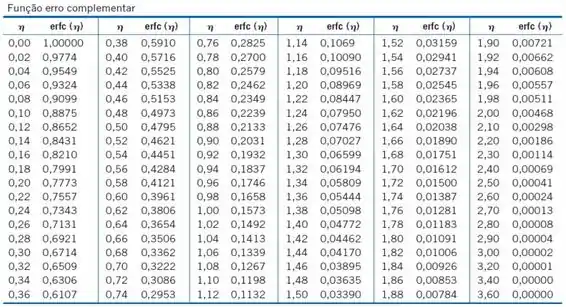
Já vimos que:

e r f c   0 = 1

Mas para achar o e r f c   2,932 nós precisamos interpolar!!

Como ɳ = 2,932 :

ɳ 1 = 2,90 → e r f c ɳ 1 = 0,00004

ɳ 2 = 3,00 → e r f c ɳ 2 = 0,00002

Se lembram da interpolação?

e r f c   ( 2,932 ) = e r f c ɳ 1 + ɳ - ɳ 1 e r f c ɳ 2 - e r f c ɳ 1 ɳ 2 - ɳ 1

Substituindo:

e r f c   ( 2,932 ) = 0,00004 + 2,932 - 2,9 0,00002 - 0,00004 3,0 - 2,9

e r f c   2,932 = 3,36 × 10 - 5

Na fórmula do Passo 1:

T s - 15 ° C 1200 ° C - 15 ° C = 1 - e 8,596 3,36 × 10 - 5

T s = 983,74 ° C

Então a temperatura do solo será 983,74 ° C   ‼

Passo 3

Para a letra (b) nós queremos fluxo de calor!

Essa é fácil, não?

Basta usarmos:

q s ˙ = h T ∞ - T s

Sabemos que:

h = 3500 W m 2 K

T ∞ = 1200 ° C

T s = 983,74 ° C

Agora é só calcular:

q s ˙ = 3500 W m 2 K 1200 ° C - 983,74 ° C

q s ˙ = 759610 W m 2

Ou melhor:

q s ˙ = 759,61 k W m 2

The end!!

Resposta

  1. 983,74 ° C ;
  2. 759,61 k W m 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Eixos de aço-carbono ( A I S I1010 ) com 0,1m de diâmetro são tratados termicamente pelo aquecimento em fornalhas a gás onde os gases se encontram a 1200K e mantêm um coeficiente convectivo de 100 W m
Uma folha de cobre, com espessura 2 L=2m m , tem uma temperatura inicial de T i = 118 ° C . Ela é subitamente imersa em água líquida, resultando em ebulição em suas duas superfícies. Para a ebulição,
Processos em batelada são frequentemente usados em operações químicas e farmacêuticas para obter uma composição química desejada no produto final e tipicamente envolvem uma operação de aquecimento tra
Em um experimento de processamento de material realizado a bordo do ônibus espacial, uma esfera de nióbio, com um revestimento com 10m m de diâmetro, é removida de um forno a 900 ° C e resfriada até u
A parede plana de uma fornalha é fabricada em aço-carbono não ligado ( k=60W / ( m·K ) , ρ=7850k g / m 3 ,c=430J / ( k g·K ) ) e tem uma espessura L=10m m . Para proteger essa parede dos efeitos corro