Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 109

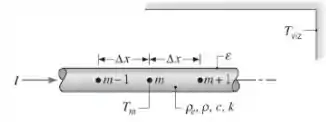
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada através do bastão, que tem uma resistividade elétrica r e e uma emissividade ε . Outras propriedades termofísicas pertinentes estão identificadas na figura. Deduza a equação de diferenças finitas, em regime transiente, para o nó m .

Passo 1

Vamos para mais uma questão \o/. Aqui nós temos um bastão fino de diâmetro D , inicialmente em equilíbrio com seu entorno, T v i z ,que repentinamente passa por uma corrente I.

O bastão está no compartimento a vácuo e possui resistência elétrica prescrita, e outras propriedades termofísicas. E a partir disso queremos encontrar a equação transitória de diferenças finitas para o nó m .

Passo 2

Para resolver essa questão vamos assumir que:

(1) A condução transitória e unidimensional no bastão;

(2) Os arredores são muito maiores que o bastão;

(3) As propriedades são constantes e avaliadas a uma temperatura média;

(4) Não há convecção dentro do compartimento a vácuo.

A equação da diferença finita é derivada do requisito de conservação de energia no volume de controle,   A c x , onde,

A c = π D 2 4

E,

P = π D

O balanço de energia tem a forma:

E ˙ e n t - E ˙ s a i + E ˙ g = E ˙ s t

q a + q b - q r a d + I 2 R e = c V T m p + 1 - T m p t

Onde,

E ˙ g = I 2 R e e R e = e x A c

Passo 3

Usando a lei de Fourier para expressar os termos de condução, q a e q b e a Eq. 1.7 para o termo de troca de radiação, q r a d , encontramos:

k A c T m - 1 p - T m p x + k A c T m + 1 p - T m p x - P x T m 4 , p - T v i z 4 + I 2 e x A c =   c A c x T m p + 1 - T m p t

Dividindo cada termo por c A c x / t , resolvendo para T m p + 1 e rearranjando a equação, obtemos:

                                    T m p + 1 = k   c × t x 2 T m - 1 p + T m + 1 p - 2 k   c × t x 2 - 1 T m p - P A c × t   c T m 4 , p - T v i z 4 + e I 2 A c 2 × t   c

Passo 4

Sabendo que F o =   t / x 2 ,   e reagrupando nós temos:

T m p + 1 = F o T m - 1 p + T m + 1 p + ( 1 - 2 F o ) T m p - P x 2 k A c F o T m 4 , p - T v i z 4 + x 2 e I 2 k A c 2 F o

O critério de estabilidade é baseado no coeficiente T m p , termo escrito como F o ≤   ½ .

Resposta

T m p + 1 = F o T m - 1 p + T m + 1 p + ( 1 - 2 F o ) T m p - P x 2 k A c F o T m 4 , p - T v i z 4 + x 2 e I 2 k A c 2 F o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva pelo método de diferenças finitas, o PVC y ' ' + 2 y ' + y = x y ( 0 ) = 2 y ( 1 ) = 0 usando h = 0.25.
Formule, por diferenças finitas, sistemas de equações cuja solução aproxime a solução dos seguintes problemas de contorno: y ' ' = y s e n ( y ) + t y y ( 0 ) = 1 y ( 1 ) = 5 y ' ' = 2 y + y 3 - t y (
Considere a rede para um sistema bidimensional sem geração volumétrica interna com temperaturas nodais mostradas abaixo. Se o espaçamento da grade for de 100m m e a condutividade térmica do material f
Considere a ferramenta de corte do Problema 4.40, mas com um ângulo de ponta de 60 ° . Derive a equação de diferença finita nodal para o nó m ,n .
Em livros-texto sobre CFD [5, 23-27], frequentemente se substitui os lados esquerdos da equação (8.119b e c) pelas duas expressões seguintes, respectivamente: ∂ ∂ x u 2 + ∂ ∂ y ( v u ) ∂ ∂ x u v + ∂ ∂