Deduza a equação de diferenças finitas, bidimensional e transiente, para a temperatura no ponto nodal localizado sobre a fronteira entre dois materiais diferentes.
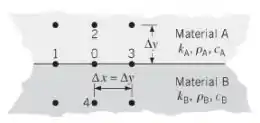
Passo 1
Aqui nós temos um ponto nodal localizado na fronteira entre dois materiais A e B. E queremos encontrar a equação de diferença finita transitória explícita bidimensional, beleza? Então vamos lá!
Passo 2
Para resolver essa questão vamos assumir que a condução é bidimensional, não tem geração de calor e as propriedades são constantes (diferentes em cada material).
Realizamos um balanço de energia no volume de controle em torno do nó 0 obtendo:
Usando como exemplo temos:
Onde é a profundidade da página. As quantidades e podem ser encontradas da mesma forma. Então é dado por
E pode ser encontrado de forma similar.
Passo 3
O termo de armazenamento é dado por:
E similarmente para
A combinação das equações produz:
Reorganizando isso, encontramos:
Onde,
e
Repara que aqui.