Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 4

Um modelo simples de escoamento para um bocal convergente bidimensional é a distribuição

u = U 0 1 + x L         v = - U 0 y L             w = 0

(a) Faça um esboço de algumas linhas de corrente na região 0 < x / L < 1 e 0 <   y / L < 1 , usando o método da Seção 1.11 . (b) Encontre expressões para as acelerações horizontal e vertical. (c) Onde está a maior aceleração resultante e qual é seu valor numérico?

Passo 1

E aí, tudo bem? Bora matar essa questão comigo!

a)

Bem, vamos usar o método da seção 1.11 para encontrar uma expressão para as linhas de corrente, teremos o seguinte:

d x u = d y v

Integrando:

∫ d x U 0 1 + x L = - ∫ d y U 0 y L

A partir dessa parte, teremos que cometer um pequeno erro na integral para entregar a resposta adequada a que a questão pede, pois na verdade:

- ∫ d y y L = L ln ⁡ 1 y

Mas teremos de fazer essa integral por substituição, assim:

- ∫ d u u

u = y L

d y = L ⋅ d u

- L ∫ d u u = - L ln ⁡ u

- ∫ d y y L = L ln ⁡ L y

Voltando, como U 0 é fator comum, podemos cancelar ele, assim:

L ⋅ ln ⁡ 1 + x L = - L ⋅ ln ⁡ y L + C

Fazendo a mesma coisa com L e aplicando a exponencial:

1 + x L = L y + C

y L = C 1 + x L

Finalmente desenhando as linhas de corrente, temos:

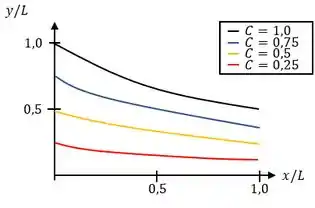
Passo 2

b)

Calculando a aceleração, da equação 4.2 temos:

a x = u ∂ u ∂ x + v ∂ u ∂ y = U 0 1 + x L ⋅ U 0 L + 0 = U 0 2 L 1 + x L

a y = u ∂ v ∂ x + v ∂ v ∂ y = 0 + - U 0 y L - U 0 L = U 0 L 2 y

Passo 3

c)

Pra matar essa de vez, só precisamos calcular o módulo da aceleração, assim:

a = a x 2 + a y 2

a = U 0 2 L 1 + x L 2 + U 0 L 2 y 2

a = U 0 4 L 2 x L 2 + 2 x L + 1 + U 0 4 L 4 y 2

Vamos chamar x / L de η e substituir y / L por C / ( 1 + x / L ) :

a = U 0 2 L η 2 + 2 η + 1 + 1 L 2 C 1 + η 2

A aceleração máxima vai ocorrer em x = L , assim:

a m á x = U 0 2 L 4 + C 2 4 L 2

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

a)

Gráfico vide passo a passo

b)

a x = U 0 2 L 1 + x L                 a y = U 0 L 2 y

c)

Em x = L

a m á x = U 0 2 L 4 + C 2 4 L 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aproximação razoável para a camada-limite laminar incompressível bidimensional sobre a superfície plana da Figura P 4.17 é u = U 2 y δ - y 2 δ 2p a r ay ≤ δe mq u eδ = C x 1 2 ,C = c o n s t (a) A
O ar escoa sob condição permanente, aproximadamente unidimensional, por um bocal cônico na Figura P4.21. Se a velocidade do som é aproximadamente 340 m/s, qual é a razão mínima de diâmetros do bocal D
Um campo de escoamento no plano xy é descrito por u = U 0 = c o n s t a n t e ,v = V 0 = c o n s t a n t e . Converta essas velocidades em coordenadas polares planas, v r e v θ .
Um escoamento incompressível em coordenadas polares é dado por v r = K cos ⁡ θ 1 - b r 2 v θ = - K sen ⁡ θ 1 + b r 2 Esse campo satisfaz a continuidade? Para a consistência, quais devem ser as dimensõ
Um tanque com volume γ contém gás nas condições ( ρ 0 ,p 0 ,T 0 ) . No instante t = 0 , é feito nele um pequeno furo de área A. De acordo com a teoria do Capítulo 9, o escoamento em massa para fora po