Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 25

Um escoamento incompressível em coordenadas polares é dado por

v r = K cos ⁡ θ 1 - b r 2

v θ = - K sen ⁡ θ 1 + b r 2

Esse campo satisfaz a continuidade? Para a consistência, quais devem ser as dimensões das constantes K e b? Faça um esboço da superfície em que v r = 0 e interprete.

Passo 1

Simbora lá fazer essa ai!

Substituindo as coordenadas polares na equação da continuidade, teremos que:

1 r ∂ ∂ r r v r + 1 r ∂ v θ ∂ θ = 0

1 r ∂ ∂ r K cos ⁡ θ 1 - b r 2 + 1 r ∂ ∂ θ - K sen ⁡ θ 1 + b r 2 = 0  

Vamos fazer uma análise de dimensões! Olha só, a velocidade é dada por m/s, certo? Então K tem de ter unidades de velocidade, porque dentro do termo, não teremos unidade! Olha só, no termo:

1 ± b r 2

r é dado por m, ele está sendo elevado ao quadrado, assim, b tem de ter uma unidade de m elevado ao quadrado também!

Assim,

K = L t = m / s

b = L 2 = m 2

Passo 2

Vamo fazer nosso esqueminha! Teremos um círculo com raio r = b , assim:

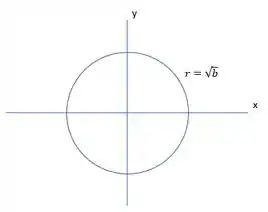
Teremos que v r = 0 quando estivermos no raio máximo ou ao longo do eixo y!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

In an axisymmetric flow, nothing varies with θ, and theonly nonzero velocities are υr and υz (see Fig. 4.2). If theflow is steady and incompressible and υz 5 Bz, where B isconstant, find the most gene
Deslocamento de inteiros à direita. Escreva um
For an incompressible plane flow in polar coordinates, weare givenυr 5 r3 cos θ 1 r2 sin θFind the appropriate form of circumferential velocity forwhich continuity is satisfied.
Flow through the converging nozzle in Fig. P4.2can be approximated by the one-dimensional velocitydistributionu (a) Find a general expression for the fluid acceleration inthe nozzle. (b) For the speci
It is desired to pump ethanol at 208C through 25 m ofstraight smooth tubing under laminar-flow conditions,Red 5 ρVd/µ , 2300. The available pressure drop is10 kPa. (a) What is the maximum possible mas