Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 37

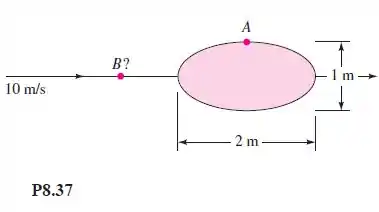
Uma oval de Rankine de 2 m de comprimento e 1 m de altura é imersa em uma corrente   U ∞ =   10   m / s , como na Figura P8.37. Avalie (a) a velocidade no ponto A e (b) a localização do ponto B onde uma partícula que se aproxima do ponto de estagnação atinge a sua máxima desaceleração.

Passo 1

Bora pra mais uma!

  1. Com L/h=2,0, podemos utilizar a equação 8.30 para encontrar o coletor de origem da fonte:

    2. h a = cot ⁡ h a 2 m U ∞ a   ;     L a = 1 + 2 m U ∞ a 1 2

    Que nos resulta em:

    L h = 2     s e m U ∞ a = 0,3178

    Enquanto isso,

    h a = 0,6395     e L a = 1,2789 → a = 1 1,2789 = 0,782 m

    Além disso V m a x U ∞ = 1,451 → V m a x = 1,451 * 10 = 14,5 m s .

  2. Ao longo do eixo x, para qualquer x ≤ - L , a velocidade em direção ao nariz do corpo tem a forma:

u = U ∞ + m a + x + m a - x ,           o n d e   m ≅ 0,3178 U ∞ a  

Então

d u d t = u ∂ u ∂ x = U ∞ + m a + x + m a - x - m 1 a - x 2 - 1 a - x 2

Para este valor de m, a desaceleração máxima ocorre em x=-1,41a. Que fica bem próximo do nariz (que está em x=-1,28a).

Resposta

  1. V m a x = 14,5 m s
  2. X = - 1,28 a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água flui através de um tubo inclinado, longo e reto, de diâmetro D e comprimento L (Figura P9-112).Não há nenhum gradiente de pressão entre os pontos 1 e 2 ;em outras palavras, a água flui através do
Considere o seguinte campo de velocidade permanente, tridimensional em coordenadas cartesianas: V → = u ,v ,w = a x z 2 - b y i → + c x y z j →+ d z 3 + e x z 2 k → onde a , b , c , d e e são constant
O escoamento se separa em um canto agudo ao longo de uma parede e forma uma bolha de separação recirculante conforme mostra a Figura P9-59 (são mostradas as linhas de corrente). O valore da função cor
Um estudante de graduação está processando seu código de C F D para seu projeto de pesquisa de mestrado e gera um gráfico das linhas de corrente de um escoamento (contornos de função corrente constant
São mostrados linhas de emissão na Figura P 9 - 61 para escoamento de água sobre a parte dianteira de um cilindro rombudo, axissimétrico alinhado com o escoamento. As linhas de emissão são geradas int