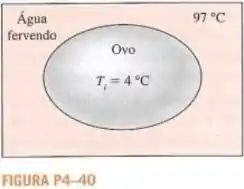
Um ovo comum pode ser tratado como uma esfera de de diâmetro cujas propriedades são aproximadamente e . O ovo está inicialmente a uma temperatura uniforme de e é colocado na água fervente a . Considerando o coeficiente de transferência de calor por convecção , determine o tempo necessário para o centro do ovo chegar a .

Nesse problema, vamos considerar que a condução de calor no ovo é unidimensional por causa da simetria sobre o ponto médio e as propriedades térmicas do ovo são constantes. Assim, o número da Biot para esse processo é:

Substituindo os dados fornecidos no enunciado, temos:

Como o número de Biot é maior que , a análise do sistema aglomerado não é aplicável. 

Vamos então resolver o problema usando a solução de termo único. Com o numero de Biot encontrado, podemos obter os coeficientes e correspondentes ao número de Biot , na tabela 4-2.

Para este número Biot, precisamos fazer uma interpolação.

Agora, podemos então usar a solução para condução transiente unidimensional em uma esfera de raio submetido à condução em todas as superfícies. Devido estamos interessado na temperatura no cento do ovo, podemos usar a seguinte equação:

Substituindo os valores fornecidos e encontrados nos passos anteriores, temos:

Temos que , portanto, a solução aproximada de um termo é aplicável. Então, o tempo que levará para o centro do ovo alcançar  é determinado pelo número de Fourier. Assim temos:

Isolando na equação.

Substituindo os valores.

Portanto, o tempo necessário para o centro do ovo chegar a  é .