Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 83

O padrão de escoamento em lubrificação de mancais pode ser ilustrado como abaixo, em que um óleo viscoso ( ρ , μ ) é forçado para dentro do espaço h(x) entre um bloco deslizante fixo e uma parede que se move à velocidade U. Se o espaçamento for finito, h

u = 1 2 μ d p d x y 2 - y h + U 1 - y h

Em que h = h(x) pode ser um espaçamento arbitrário que varia lentamente.

Passo 1

Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos? Bem, o enunciado nos diz que temos u(y) e uma p(x), então isso quer dizer que vamos precisar da componente onde temos o gradiente de pressão na direção x, ou seja!!

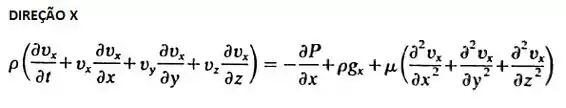
Passo 2

No desenho é mostrado que temos o fluido apenas indo na direção x, certo? E considerando um escoamento unidimensional, temos então que as componentes nas outras direções serão zero, ou seja, v y = v z = 0 . No enunciado ele chama de componente v e w, beleza? Mas aqui vamos chamar de v y   e   v z para você se acostumar também com outros tipos de notação! Além disso, temos que o escoamento está completamente desenvolvido, então ∂ ∂ x = 0 para qualquer componente da velocidade. O enunciado também diz para desprezarmos o termo gravitacional. Isso reduz nossa equação na seguinte forma:

ρ d v x d t = - d p d x + μ ∂ 2 v x ∂ y 2 → c o n s i d e r a n d o   r e g i m e   e s t a c i o n á r i o → d 2 v x d y 2 = 1 μ d p d x

De um lado temos uma função que varia com y e do outro lado uma função que varia com x, então para que elas sejam iguais, elas devem ser iguais a uma constante, certo?

d 2 v x d y 2 = 1 μ d p d x = C

Passo 3

Integrando duas vezes

d 2 v x d y 2 = 1 μ d p d x = 1 μ Δ p Δ x

d v x d y = 1 μ Δ p Δ x y + C 1

v x y = 1 μ Δ p Δ x y 2 2 + C 1 y + C 2

Com as condições de contorno sendo

u 0 = U → C 2 = U

u h = 0

1 μ Δ p Δ x h 2 + C 1 h + U = 0

C 1 = - U + 1 μ Δ p Δ x h 2 h  

Substituindo as constantes e rearranjando elas, temos que:

v x = 1 2 μ Δ p Δ x y 2 - y h + U 1 - y h

Resposta

v x = 1 2 μ Δ p Δ x y 2 - y h + U 1 - y h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O campo de velocidade para uma linha de fontes no plano r θ (Figura P 4 - 39 ) é dado por u r = m 2 π r u θ = 0 Onde m é a intensidade da linha de fontes. No caso com m 2 π = 1.0m 2 / s , faça um gráf
Considere o campo de velocidade em regime permanente, incompressível e bidimensional do Problema 4 - 35 ( a ) Calcule a aceleração material no ponto ( x = 2m ,y = 3m ) ( b ) Esboce os vetores aceleraç
Um campo de velocidade bidimensional, incompressível e em regime permanente é dado por V → = u , v = 1 + 2.5 x + y i → + - 0.5 - 1.5 x - 2.5 y j → Onde as coordenadas x e y estão em m e o módulo da ve
Vamos analisar o cilindro rotatório parcialmente cheio da Figura 2.23 como um problema de rotação, iniciando do repouso e prosseguindo até atingir a torração de corpo sólido. Quais são as condições de
Para o filme líquido sendo drenado na Figura P4.36, quais são as condições de contorno apropriadas (a) no fundo em y = 0 e (b) na superfície em y = h ?