Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 1
A parede plana unidimensional da Figura 3.1 tem espessura e condutividade térmica . As temperaturas do fluido são e , respectivamente. Usando os valores máximo e mínimo típicos dos coeficientes de transferência de calor por convecção listados na Tabela 1.1, determine os fluxos térmicos, em regime estacionário, mínimos e máximos através da parede para (i) convecção natural em gases, (ii) convecção natural em líquidos, (iii) convecção forçada em gases, (iv) convecção forçada em líquidos, e (v) convecção com mudança de fase.
Passo 1
Se não bastasse procurarmos a Figura em outro capítulo, temos que buscar uma tabela também. Eita trabalho!
O bom é que este é o único trabalho, basicamente.
A questão nos pede para determinar o fluxo térmico (máximo e mínimo) em diferentes situações. Se formos lá na Figura 3.1, temos o desenho esquemático do processo representado pelas seguintes resistências térmicas:
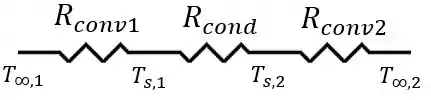
Então, podemos escrever o fluxo térmico através da seguinte relação:
Passo 2
Certo, mas quais os valores de e ? Estes valores nós temos que obter da tabela 1.1. Lá, temos os seguintes valores:
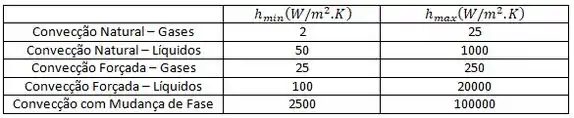
Então, se queremos obter o maior fluxo para um determinado caso, usamos , e se queremos o menor fluxo, usamos .
Sendo assim, temos os seguintes valores:
Para convecção natural com gases:
Para convecção natural com líquidos:
Para convecção forçada com gases:
Para convecção forçada com líquidos:
Para convecção com mudança de fase:
E assim terminamos a questão!
Resposta
Para convecção natural com gases:
Para convecção natural com líquidos:
Para convecção forçada com gases:
Para convecção forçada com líquidos:
Para convecção com mudança de fase: