Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas Abrangentes - Ex. 3
Um pequeno escorregador de água deve ser instalado em uma piscina. Veja a Figura PA6.3. O fabricante do escorregador recomenda uma vazão contínua Q de água de 1,39 x 10−3 m3/s (aproximadamente 22 gal/min) pelo escorregador, para assegurar que as pessoas não esquentem seus traseiros. Uma bomba deve ser instalada debaixo do escorregador, com uma mangueira de 5,00 m de comprimento e 4,00 cm de diâmetro fornecendo água da piscina para o escorregador da piscina. A bomba tem 80% de rendimento e está completamente submersa a 1,00 m da superfície da água. A rugosidade interna da mangueira é de aproximadamente
0,0080 cm. A mangueira descarrega a água no topo do escorregador como um jato livre aberto à atmosfera. A saída da mangueira está a 4,00 m acima da superfície de água. Para escoamento turbulento totalmente desenvolvido, o fator de correção da energia cinética é aproximadamente 1,06. Ignore qualquer perda localizada. Considere que rho = 998 kg/m3 e nu= 1,00 x 10−6 m2/s para a água. Determine a potência de acionamento (ou seja, a potência real de eixo em watts) necessária para a bomba.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nesse problema, temos água a (, ) escoando em um escorregador a uma vazão de .
Uma bomba com de rendimento deve ser instalada a abaixo do escorregador com uma mangueira de comprimento e diâmetro , que descarrega água com um jato livre aberto à atmosfera, com essa saída a acima da superfície da água.
A questão pede que a gente calcule a potência real da bomba em watts.
Pra isso, vamos fazer um balanço de energia nesse sistema, calcular o fator de atrito e, por fim, determinar a potência requerida para a bomba.
Então vem comigo que a gente vai resolver esse problema juntos!
Passo 2
Em primeiro lugar, vamo fazer um balanço de energia pra esse sistema.
O balanço de energia para o sistema, partindo da superfície livre até a saída da mangueira é:
Sendo: e a distância d saída da mangueira até a superfície livre, é a pressão atmosférica, que é igual nos dois pontos do volume de controle, e , pois não há escoamento nesse ponto da superfície livre.
Além disso, sabemos que a perda de carga é expressa como .
Reorganizando a equação, teremos uma expressão para a carga da bomba:
Sendp , o fator de correção da energia cinética para o escoamento turbulento totalmente desenvolvido.
Passo 3
Antes de prosseguir para o final, precisamos calcular o fator de atrito de Darcy, considerando a rugosidade relativa de .
Além disso, vamo precisar calcular o número de Reynolds. Pra isso, vamos calcular :
E o número de Reynolds:
Com o número de Reynolds e a rugosidade relativa a gente vai entrar no diagrama de Moody pra calcular o fator de atrito:
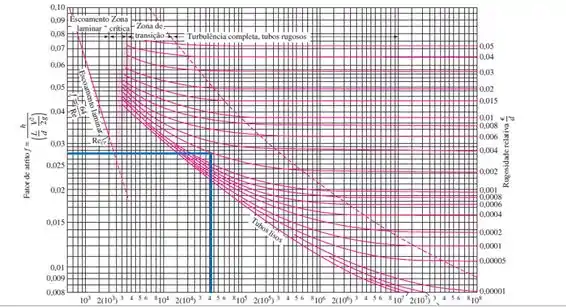
Dessa forma, achamos .
Passo 4
Agora podemos calcular a carga da bomba:
Pra calcular a potência requerida da bomba em watts, com uma eficiência de , devemos fzer uma análise dimensional:
Pronto, matamos o problema juntos!
Resposta
A potência de acionamento necessária para a bomba é