Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 85
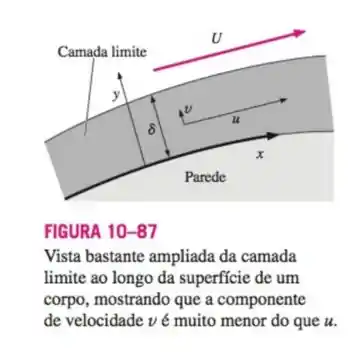
O perfil de Blasius da camada limite é uma solução exata das equações da camada limite para escoamento sobre uma placa plana. No entanto, os resultados são um pouco incômodos de usar, pois os dados aparecem em forma tabular (a solução é numérica). Assim, uma aproximação de uma onda senoidal simples (Figura ) é usada frequentemente no lugar da solução de Blasius, isto é, para , e para , onde a espessura da camada limite. Coloque em um mesmo gráfico o perfil de Blasius e a aproximação da onda senoidal, na forma adimensional ( versus ) e compare. O perfil da onda senoidal é uma aproximação razoável?
Passo 1
Pela aproximação senoidal temos que:
Ou seja:
Agora a solução de Blasius pode ser entendida como:
Juntando as duas equações teremos:
E que:
Onde pela tabela .
E para isso temos que saber usar a tabela esquisita 10-3 que é obtida por cálculo numérico da equação diferencial descrita no exemplo 10-10 (todas as referências estão na primeira edição desse livro tá?).
Passo 2
Então plotando os dois gráficos nós temos:
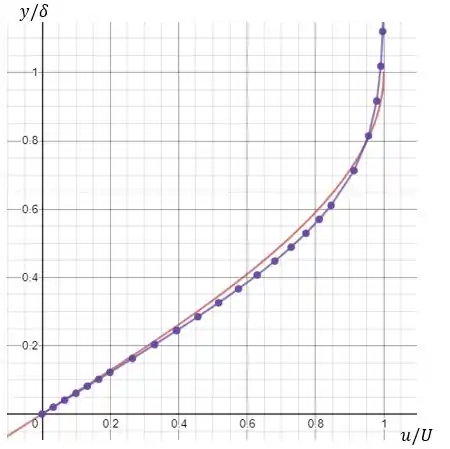
Onde a linha vermelha é a aproximação senoidal (que vai de até ) e a linha roxa (com os pontinhos) é a solução de Blasius, para ver o gráfico como fico acesse encurtador.com.br/kBRV0. Onde e na equação senoidal.
Note que a aproximação é bem razoável , ela está bem próxima da solução de Blasius, porém ela se limita apenas no intervalo de
Resposta
Gráfico do passo 2