Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 49

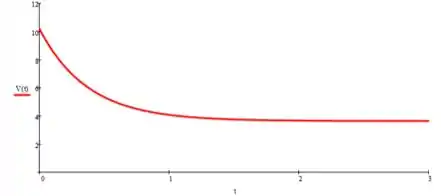
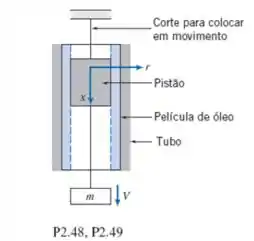
O pistão no Problema 2.48 está viajando a um terminal de velocidade, mas, agora, com uma massa m desconectada do pistão. Rastreie um gráfico com a velocidade do pistão em função do tempo. Quanto tempo o pistão leva para alcançar 1% dessa nova velocidade terminal?

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Por equilíbrio, temos que:

W = S G × ρ × g × π D 2 4 L  

Já as forças de viscosidade serão dadas pela fórmula:

F = μ 2 V D t u b o - D p i s t ã o π D p i s t ã o L

Aplicando-se a segunda lei de Newton:

m d V d t = W - F

Logo, isolando-se a derivada da velocidade, teremos:

d V d t = g - a V

Logo:

d x d t = - a X

Isso é uma equação diferencial e nosso foco aqui não é a resolução delas, portanto, só aceite a resposta que vou te dar, rsrs. Teremos algo dessa forma:

V t = V 0 - g a e - a t + g a

Plotando o gráfico, teremos:

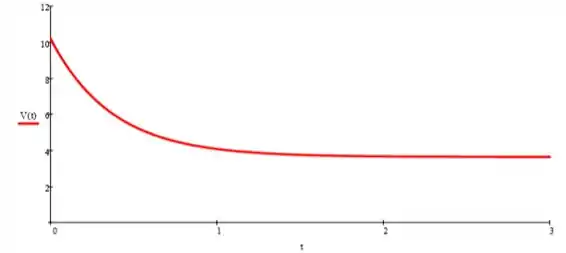
Passo 2

A segunda parte é só conta. Basta isolar o tempo e substituir a velocidade, que no caso será 1% da velocidade terminal. Substituindo os valores e isolando o tempo, teremos:

t = 1,93 s

Resposta

t = 1,93 s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de golfe americana é exibida no Problema 1.42. Para definir uma massa de bola e sua incerteza como dados, determine uma precisão com que o diâmetro da bola deve ser medido para sua massa espe
Uma bomba de tipo seringa é usada para bombear líquido a uma vazão de 100m L/m i n . O projeto para o pistão é tão incerteza na velocidade do pistão é de 0,00125c m , e o diâmetro interno do cilindro
A altura de um edifício pode ser estimada em uma distância horizontal horizontal até um ponto no solo e o ângulo desse ponto ao topo do edifício. Supondo que essas medições sejam L=30±0,15m e θ=30±0,2
A variação da viscosidade do ar com a temperatura é bem correlacionada pela equação empírica de Sutherland μ = b T 1 2 1 + S T Os valores de b e S que melhor ajustam essa equação são dados no Apêndice
A variação da viscosidade do ar com a temperatura é bem correlacionada pela equação empírica de Sutherland μ = b T 1 2 1 + S T Os valores de b e S que melhor ajustam esta equação são dados no Apêndice