Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 16

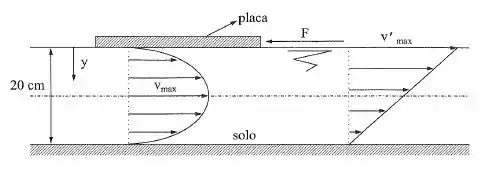
A placa da figura tem uma área de 2   m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa formando um diagrama de velocidades bidimensional dado por v = 20 y v m á x ( 1 - 5 y ) . A viscosidade dinâmica do fluido é 10 - 2 N ⋅ s / m 2 e a velocidade máxima é 2   m / s .

  1. Qual é o gradiente de velocidade junto ao solo?
  2. Qual é a força necessária para manter a placa em equilíbrio estático?
  3. Qual é a velocidade média?
  4. Fora do contato da placa, o diagrama de velocidades é considerado linear bidimensional. Qual é a velocidade máxima?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Item “a”:

O gradiente de velocidade é dado pela derivada da equação da velocidade:

v = 20 v m á x y - 100 v m á x y 2

A sua derivada é dada por:

d v d y = 20 v m á x - 2 00 v m á x y

Aplicando em y = 0,2   m , temos que:

d v d y = 20 ( 2 ) - 200 ( 2 ) ( 0,2 )

d v d y = - 40   s - 1

Passo 2

Item “b”:

Para y = 0 , temos que o perfil de velocidade é dado por:

d v d y = 20 ( 2 ) - 200 ( 2 ) ( 0 )

d v d y = 40   s - 1

Sabendo o perfil, temos que:

τ = μ d v d y

τ = 10 - 2 40

τ = 0,4   N

A força é dada pelo produto da tensão pela área, logo:

F = τ A

F = 0,4 2

F = 0,8   N

Passo 3

Item “c”:

A equação da velocidade média para um escoamento bidimensional é:

v m = 1 b h ∫ v d A

Resolvendo, temos que:

v m = 1 b h ∫ 0 0,2 20 v m á x y - 100 v m á x y 2 d y

v m = 200 0,2 2 2 - 5 0,2 3 3

v m = 1,33   m / s

Passo 4

Item “d”:

Pela equação da continuidade, como a vazão de entrada é igual a de saída e as áreas das seções são iguais, temos que:

v m á x = 2 v m

Portanto:

v m á x = 2 1,33

v m á x = 2,66   m / s

Resposta

a ) d v d y = - 40   s - 1

b ) F = 0,8   N

c ) v m = 1,33   m / s

d )   v m á x = 2,66   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A distribuição de velocidades para escoamento laminar em um longo tubo circular de raio R é dada pela expressão unidimensional, V → = u i ^ = u m a x 1 - r R 2 i ^ Para este perfil, obtenha expressões
Um laboratório universitário deseja construir um túnel de vento de vazão 15 m 3 s com velocidades variáveis do ar. Para isso, propõe-se construir o túnel com uma sequência de três seções de teste circ
A área sombreada mostrada está em um escoamento onde o campo de velocidade é dado por V =a x î=b y ĵ î ĵ; a=b=1s - 1 e as coordenadas são medidas em metros. Avalie a vazão volumétrica e o fluxo de qua
Para o escoamento do Problema 4.17, obtenha uma expressão para o fluxo de energia cinética, ∫ ( V 2 2 )ρ V → d A → , através da seção normal ao eixo do tubo.
A ducha de um chuveiro alimentado por um tubo de água com diâmetro interno de 19,05 mm consiste em 50 bocais de diâmetros internos de 0,79 mm. Considerando uma vazão de 1,39× 10 - 4 m 3 s , qual é a v