Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 38

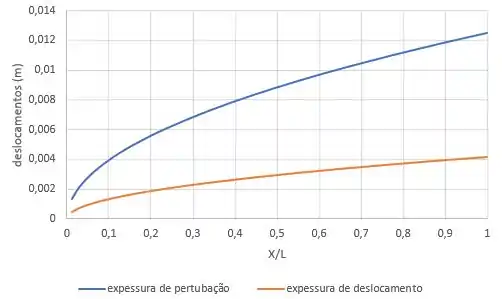
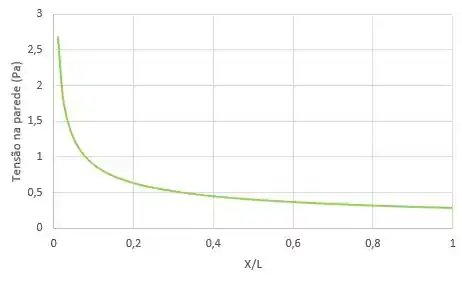
Uma placa plana delgada, de comprimento L = 0,25 m e largura b = 1 m , é instalada em um túnel de água como uma divisora de fluxo. A velocidade de corrente livre é U = 1,75   m / s e o perfil de velocidade na camda limite é aproximado como parabólico. Trace δ ,   δ * e τ w versus x / L para a placa.

Passo 1

Vamos reunir as informações que o enunciado deu:

Comprimento da placa: L = 0,25   m

Largura da placa: b = 1   m

Velocidade de corrente livre: U = 1,75   m / s

Ele também diz que o perfil de velocidade é parabólico, ou seja, segue essa equação:

u U = 2 y δ - y δ 2

Precisamos encontrar a relação de x com a expessura de pertubação ( δ ) , a expessura de deslocamento ( δ * ) e a tensão na parede ( τ w ) .

Passo 2

Encontrando primeiro a relação entre x e δ , lembramos dessa equação:

δ x = 5,48 R e x

Sabendo que:

R e x = U x ν

Podemos substituir uma na outra, jogar o x para o outro lado e arrumar:

δ = 5,48   x   ν U x = 5,48 x ν U

Usando os dados do enunciado e considerando a vicosidade cinemática da água como ν = 1,01 ⋅ 10 - 6 m 2 / s a temperatura de 20 ° C :

δ = 5,48 1.01 ⋅ 10 - 6 x 1,75

Achamos a relação entre δ e x . 😊

Passo 3

Podemos achar uma relação entre δ ( x ) e δ * , através dessa integral:

δ * = ∫ 0 δ 1 - u U d y

Sabendo que:

u U = 2 y δ - y δ 2

É só a gente substituir uma na outra e integrar:

δ * = ∫ 0 δ 1 - 2 y δ + y 2 δ 2 d y = y - y 2 δ + y 3 δ 2 ​ 0 δ = δ - δ + δ 3 = δ 3

Logo:

δ * = δ 3 = 5,48 3 1.01 ⋅ 10 - 6 x 1,75

Uhul! Conseguimos!

Passo 4

Vamos seguir uma ideia parecida para achar τ w .

A equação da tensão na parede para o caso de uma placa plana é:

τ w = 2 μ U δ

Sabendo a expressão de δ ( x ) , os dados do enunciado e considerando μ = 1,01 ⋅ 10 - 3 N ⋅ s / m ² como viscosidade dinâmica a 20 ° C .

τ w = 2,02 ⋅ 1,75 ⋅ 10 - 3 5,48 1.01 ⋅ 10 - 6 x 1,75

Passo 5

Com todas as expressões, a gente consegue montar os gráficos que o enunciado pediu. Ficam assim oh:

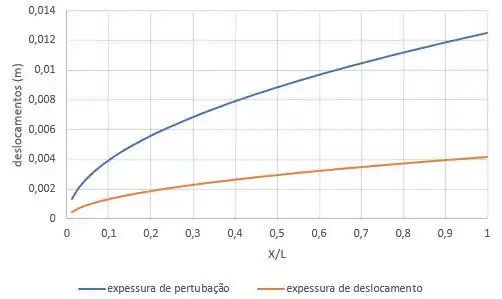
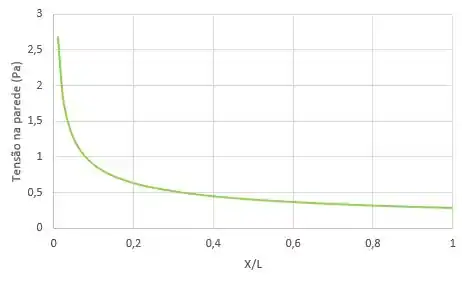
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um escoamento de ar desenvolve-se em um duto horizontal cilíndrico, com diâmetro D = 400m m , após uma seção de entrada bem arredondada. Uma camada-limite turbulenta cresce sobre a parede do duto, mas
Usando os resultados numéricos obtidos por Blasius (Tabela 9.1), avalie a distribuição de tensão de cisalhamento em uma camada limite laminar sobre uma placa plana. Trace τ / τ w versus y / δ . Compar
Um túnel de vento de laboratório tem uma seção de teste quadrada, com lados de extensão W = 305m m , e comprimento L = 610m m . Quando a velocidade de corrente livre do ar na entrada da seção de teste
Ar escoa para dentro da seção de contração de entrada de um túnel de vento de um laboratório de graduação. O ar entra em seguida na seção de teste, que é um duto de seção quadrada com lados de 305 mm.
9.17Avalieδ*/δeθ/δparaoperfildevelocidadeturbulentodaleidepotência1/7dadonoProblema9.14.Comparecomasrazões paraoperfilparabólicodevelocidadedecamada­limitelaminardadonoProblema9.10.