Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas de Projeto - Ex. 2
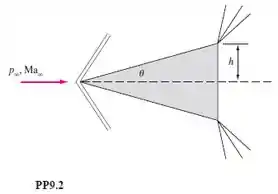
PP9.2 – Considere o escoamento supersônico de ar, nas condições ao nível do mar, em torno de uma cunha de semiângulo θ, com mostra a Fig. PP9.2. Admita que a pressão na face posterior da cunha se iguala à pressão do fluido quando ele sai do leque de Prandtl-Meyer.
A) Considere . Para qual ângulo o coeficiente de arrasto de onda supersônico CA, baseado na área frontal, será exatamente 0,5?
B) Suponha que θ = 20°. Existe um número de Mach da corrente livre para o qual o coeficiente de arrasto de onda CA, baseado na área frontal, será exatamente 0,5?
Passo 1
A)
Para respondermos essa questão vamos pegar uma equação da função de expansão supersônica de Prandtl-Meyer, cuja expressão é:
Onde, o parâmetro K é definido em função da razão de calores específicos, cuja expressão é:
A razão de calores específicos é dada por:
Onde, cp é o calor especifico a pressão constante e cv é o calor especifico a volume constante.
Para o ar, em condições de atmosférica no nível do mar, o valor de k usual é:
Passo 2
Vamos agora pegar a Eq. 9.105 do White para calcularmos o ângulo para o qual o coeficiente de arrasto é 0,5
A expressão descrita pela eq. 9.105 é:
Considerando
Assim,
Isolando o ângulo θ:
Simplificando a equação acima, vamos ter que:
Aplicando os valores:
Passo 3
O valor obtido para o ângulo se encontra em radianos, vamos então converter para graus.
Lembrando que para conversão de ângulo de radianos para graus, podemos usar o seguinte fator de conversão:
Fazendo a conversão:
Vamos obter que o ângulo em graus é:
Passo 4
B)
Para encontrarmos o nº de Mach, Ma, da corrente livre para o qual o coeficiente de arrasto de onda CA, é 0,5, vamos novamente usar a Eq.2
Vamos tentar isolar o termo do nº de Mach:
Passo 5
O ângulo θ deve estar em radianos, então precisamos fazer uma conversão de graus para radianos, de forma análoga ao que foi feito antes no item A:
Pelo fator de conversão:
Assim,
Voltando a Eq3 e aplicando os valores:
Resposta
A)
B)