Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 44

Em uma configuração cilíndrica bidimensional, os espaçamentos radiais ( ∆ r ) e angulares ( ∆ φ ) entre os pontos nodais são uniformes. O contorno em r = r , está em uma temperatura uniforme T i . Na direção radial os contornos são adiabático (isolado) e exposto a condições de convecção na superfície ( T ∞ , h ) , como ilustrado na figura. Deduza as equações de diferenças finitas para: ( i ) o ponto nodal 2 , ( i i ) o ponto nodal 3 , e ( i i i ) o ponto nodal 1 .

Passo 1

O exercício nos pede para definir a equação de diferenças finitas para três pontos nodais: 2 ,   3 e 1 . Começando pelo ponto 2 , precisamos primeiro definir o volume de controle e as taxas de transferência de calor que atingem o volume:

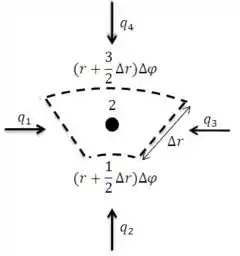
Aplicando o balanço de energia em regime estacionário:

E ˙ e n t + E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q 3 + q 4 = 0

Vamos agora descrever cada taxa separadamente, considerando que todas as taxas são transferidas por condução:

q 1 = q 1 → 2

q 1 = k A L ∆ T

q 1 = k ∆ r l r + ∆ r ∆ φ ( T 1 - T 2 )

q 2 = q ( T i ) → ( 2 )

q 2 = k A L ∆ T

q 2 = k ( r + 1 2 ∆ r ) ∆ φ l ∆ r ( T i - T 2 )

q 3 = q 3 → 2

q 3 = k A L ∆ T

q 3 = k ∆ r l r + ∆ r ∆ φ ( T 3 - T 2 )

q 4 = q 5 → 2

q 4 = k A L ∆ T

q 4 = k ( r + 3 2 ∆ r ) ∆ φ l ∆ r ( T 5 - T 2 )

Substituindo no balanço:

k ∆ r l r + ∆ r ∆ φ T 1 - T 2 + k r + 1 2 ∆ r ∆ φ l ∆ r T i - T 2 + k ∆ r l r + ∆ r ∆ φ T 3 - T 2 + k r + 3 2 ∆ r ∆ φ l ∆ r T 5 - T 2 = 0

∆ r r + ∆ r ∆ φ T 1 - T 2 + r + 1 2 ∆ r ∆ φ ∆ r T i - T 2 + ∆ r r + ∆ r ∆ φ T 3 - T 2 + r + 3 2 ∆ r ∆ φ ∆ r T 5 - T 2 = 0

∆ r 2 r + ∆ r ∆ φ 2 T 1 - T 2 + r + 1 2 ∆ r T i - T 2 + ∆ r 2 r + ∆ r ∆ φ 2 T 3 - T 2 + r + 3 2 ∆ r T 5 - T 2 = 0

∆ r 2 r + ∆ r ∆ φ 2 T 1 + T 3 + r + 1 2 ∆ r T i + r + 3 2 ∆ r T 5 - 2 ∆ r 2 r + ∆ r ∆ φ 2 + r + ∆ r T 2 = 0

Passo 2

Vamos realizar um procedimento análogo para o ponto nodal 3 . Para começar, devemos definir o volume de controle:

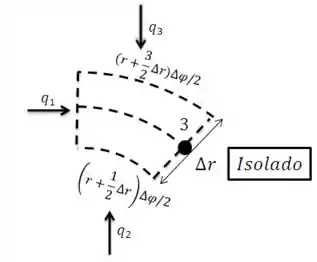
Aplicando o balanço de energia em regime estacionário:

E ˙ e n t + E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q 3 = 0

Vamos agora descrever cada taxa separadamente, considerando que todas as taxas são transferidas por condução:

q 1 = q 2 → 3

q 1 = k A L ∆ T

q 1 = k ∆ r l r + ∆ r ∆ φ ( T 2 - T 3 )

q 2 = q ( T i ) → ( 3 )

q 2 = k A L ∆ T

q 2 = k ( r + 1 2 ∆ r ) ∆ φ l 2 ∆ r ( T i - T 3 )

q 3 = q 6 → 3

q 4 = k A L ∆ T

q 3 = k ( r + 3 2 ∆ r ) ∆ φ l 2 ∆ r ( T 6 - T 3 )

Substituindo no balanço:

k ∆ r l r + ∆ r ∆ φ ( T 2 - T 3 ) + k ( r + 1 2 ∆ r ) ∆ φ l 2 ∆ r ( T i - T 3 ) + k ( r + 3 2 ∆ r ) ∆ φ l 2 ∆ r ( T 6 - T 3 ) = 0

∆ r r + ∆ r ∆ φ ( T 2 - T 3 ) + ( r + 1 2 ∆ r ) ∆ φ 2 ∆ r ( T i - T 3 ) + ( r + 3 2 ∆ r ) ∆ φ 2 ∆ r ( T 6 - T 3 ) = 0

2 ∆ r 2 r + ∆ r ∆ φ 2 ( T 2 - T 3 ) + r + 1 2 ∆ r ( T i - T 3 ) + r + 3 2 ∆ r ( T 6 - T 3 ) = 0

2 ∆ r 2 r + ∆ r ∆ φ 2 T 2 + r + 1 2 ∆ r T i + r + 3 2 ∆ r T 6 - 2 ∆ r 2 r + ∆ r ∆ φ 2 + r + ∆ r T 3 = 0

Passo 3

Por fim, vamos para a equação de diferenças finitas para o nó 1. O volume de controle será:

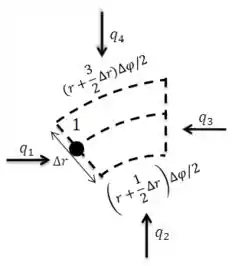
Aplicando o balanço de energia em regime estacionário:

E ˙ e n t + E ˙ s a í d a + E ˙ g e r = 0

E ˙ e n t = 0

q 1 + q 2 + q 3 + q 4 = 0

Vamos agora descrever cada taxa separadamente:

q 1 = q c o n v

q 1 = h A ∆ T

q 1 = h ∆ r l ( T ∞ - T 1 )

q 2 = q ( T i ) → ( 1 )

q 2 = k A L ∆ T

q 2 = k r + 1 2 ∆ r ∆ φ 2 l ∆ r ( T i - T 1 )

q 3 = q 2 → 1

q 3 = k A L ∆ T

q 3 = k ∆ r l r + ∆ r ∆ φ ( T 2 - T 1 )

q 4 = q 4 → 1

q 4 = k A L ∆ T

q 4 = k r + 3 2 ∆ r ∆ φ 2 l ∆ r ( T 4 - T 1 )

Substituindo no balanço:

h ∆ r l ( T ∞ - T 1 ) + k r + 1 2 ∆ r ∆ φ 2 l ∆ r ( T i - T 1 ) + k ∆ r l r + ∆ r ∆ φ ( T 2 - T 1 ) + k r + 3 2 ∆ r ∆ φ 2 l ∆ r ( T 4 - T 1 ) = 0

h ∆ r ( T ∞ - T 1 ) + k r + 1 2 ∆ r ∆ φ 2 ∆ r ( T i - T 1 ) + k ∆ r r + ∆ r ∆ φ ( T 2 - T 1 ) + k r + 3 2 ∆ r ∆ φ 2 ∆ r ( T 4 - T 1 ) = 0

2 h ∆ r 2 ∆ φ ( T ∞ - T 1 ) + k r + 1 2 ∆ r ( T i - T 1 ) + 2 k ∆ r 2 r + ∆ r ∆ φ 2 ( T 2 - T 1 ) + k r + 3 2 ∆ r ( T 4 - T 1 ) = 0

2 h ∆ r 2 k ∆ φ ( T ∞ - T 1 ) + r + 1 2 ∆ r ( T i - T 1 ) + 2 ∆ r 2 r + ∆ r ∆ φ 2 ( T 2 - T 1 ) + r + 3 2 ∆ r ( T 4 - T 1 ) = 0

2 h ∆ r 2 k ∆ φ T ∞ + r + 1 2 ∆ r T i + 2 ∆ r 2 r + ∆ r ∆ φ 2 T 2 + r + 3 2 ∆ r T 4 - 2 h ∆ r 2 k ∆ φ + r + ∆ r + ∆ r 2 r + ∆ r ∆ φ 2 T 1 = 0

Resposta

( i ) Ponto 2 : ∆ r 2 r + ∆ r ∆ φ 2 T 1 + T 3 + r + 1 2 ∆ r T i + r + 3 2 ∆ r T 5 - 2 ∆ r 2 r + ∆ r ∆ φ 2 + r + ∆ r T 2 = 0

i i Ponto 3 :

2 ∆ r 2 r + ∆ r ∆ φ 2 T 2 + r + 1 2 ∆ r T i + r + 3 2 ∆ r T 6 - 2 ∆ r 2 r + ∆ r ∆ φ 2 + r + ∆ r T 3 = 0

( i i i ) Ponto 1 :

2 h ∆ r 2 k ∆ φ T ∞ + r + 1 2 ∆ r T i + 2 ∆ r 2 r + ∆ r ∆ φ 2 T 2 + r + 3 2 ∆ r T 4 - 2 h ∆ r 2 k ∆ φ + r + ∆ r + ∆ r 2 r + ∆ r ∆ φ 2 T 1 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma aleta plana com seção transversal uniforme é feita com um material de condutividade térmica igual a 50 W m K , tem espessura w = 6 mm e comprimento de L = 48 mm, e é muito grande na direção normal
Seja o sistema para resfriamento de turbina a gás mostrado no Exemplo 4.3. No Problema 3.23 são descritas vantagens associadas à aplicação de um revestimento de barreira térmica (RBT) sobre a superfíc
Uma placa de grande espessura, com difusividade térmica de 5,6×10 - 6m 2 / s e condutividade térmica de 20W / ( m·K ) , está inicialmente a uma temperatura uniforme de 325 ° C . De repente, a sua supe
Pilares de concreto reforçados com aço são usados em grandes construções. Falhas estruturais podem ocorrer em altas temperaturas em função de um incêndio por causa do enfraquecimento do núcleo metálic
Com referência ao Comentário 4 do Exemplo 5.12 , analise a súbita exposição da superfície a uma grande vizinhança, a uma temperatura elevada ( T v i z ) , e a condições de convecção ( T ∞ ,h ) .(a) De