Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 133

O Problema 9.107 mostrou um disco circular pendurado em uma corrente de ar por meio de uma haste cilíndrica. Considere que a haste tem L   =   40   m m de comprimento e d   =   3   m m de diâmetro. Resolva o Problema 9.107, incluindo o efeito de arrasto sobre o suporte.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:

C A = F A 1 2 ρ V 2 A

∑ M → = 0

Somando os momentos:

W L   s e n α - F n 1   L - 1 2 L - D 2 F n 2 = 0

Logo, para cada força normal de arrasto:

F n = 1 2 ρ V n 2 A C A

Logo:

F n 1 = 1 2 ρ V c o s α 2 π D 2 4   C A 1

F n 2 = 1 2 ρ V c o s α 2 L - D 2 d   C A 2

Portanto, da equação 1:

M L g s e n α = 1 2 L   ρ V c o s α 2 π D 2 4 C A 1 + 1 2 L - D 2 1 2 ρ V c o s α 2 L - D 2 d C A 2

M = ρ V 2 cos ⁡ α 2 4 g s e n α 1 2 π D 2 C A 1 + 1 - D 2 L L - D 2 d C A 2

Portanto, rearranjando:

V = 4 M g ρ   t g α cos ⁡ α   1 1 2 π D 2 C A 1 + 1 - D 2 L L - D 2 d C A 2

Logo, substituindo:

V = 35,5   t g α cos ⁡ α       m / s

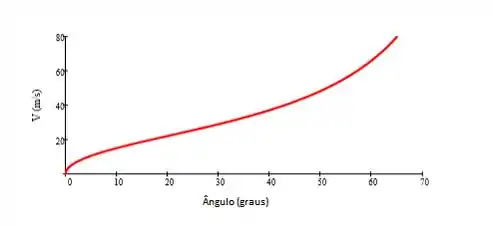
Plotando o gráfico em função do ângulo:

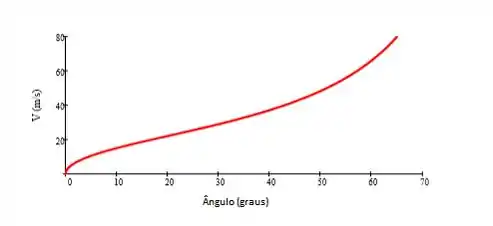
Resposta

V = 35,5   t g α cos ⁡ α       m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas bolas de aço (d = 7,86) estão conectadas por uma barra delgada articulada de peso e arrasto desprezíveis, como na Figura P7.99. Um batente impede a vara de girar no sentido anti-horário. Calcule
Os dados na Figura P7.108 referem-se a sustentação e arrasto de uma esfera girante da Referência 45. Admita que uma bola de tênis (P = 0,56 N, D = 6,35 cm) seja golpeada ao nível de mar com velocidade
Um automóvel tem massa de 1.000 kg e área de arrasto CAA 5 0,7 m2. A resistência de rolagem de 70 N é aproximadamente constante. O carro está se movendo em ponto morto, sem freios, a 90 km/h, quando c
Uma esfera de madeira (d = 0,65) é ligada por uma barra delgada a uma articulação em um túnel de vento, como na Figura P7.112. Ar a 20ºC e 1 atm escoa e faz a esfera levitar. (a) Plote a variação do â
Um arremessador (pitcher) de beisebol arremessa uma “bola com efeito” à velocidade inicial de 105 km/h e uma rotação de 6.500 rpm em torno de um eixo vertical. Uma bola de beisebol pesa 1,42 N e tem u