Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 18

Um vaso esférico usado como um reator para produzir fármacos tem uma parede de aço inoxidável k   =   17 W m   ·   K com 5   m m de espessura e diâmetro interno D i =   1,0   m . Durante a produção, o vaso contém reagentes para os quais ρ   =   1100 k g m 3 e c   =   2400 J k g   ·   K , enquanto reações exotérmicas liberam energia a uma taxa volumétrica de q ˙ =   104 W m 3 . Como uma primeira aproximação, os reagentes podem ser considerados misturados idealmente e a capacitância térmica do vaso pode ser desprezada.

(a) A superfície externa do vaso está exposta ao ar ambiente T ∞   =   25 ° C , no qual pode-se admitir um coeficiente de transferência de calor h   =   6 W m 2   ·   K . Sendo a temperatura inicial dos reagentes igual a 25 ° C , qual é a temperatura dos reagentes após cinco horas de processamento? Qual é a temperatura correspondente na superfície externa do vaso?

(b) Explore o efeito de variar o coeficiente convectivo nas condições térmicas transientes no interior do reator.

Passo 1

Vamos lá! Nosso problema nos pede a temperatura dos reagentes após o processo e a temperatura externa do vaso, mas antes que tal desenharmos um esboço do comportamento desse problema pra entendermos o que o ocorre. Fica assim.

Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - O s   r e a g e n t e s   m i s t u r a d o s   i d e a l m e n t e   p o s s u e m   a   m e s m a   t e m p e r a t u r a   e

p o s s u e m   t e m p e r a t u r a   i g u a l   a   t e m p e r a t u r a   d a   s u p e r f i c i e   i n f e r i o r   d o   v a s o

I I - C a p a c i t â n c i a   t e r m i c a   d o   v a s o   p o d e   s e r   d e s p r e z í v e l

I I I - T r o c a   p o r   r a d i a ç ã o   d e s p r e z í v e l

I V - p r o p r i e d a d e s   c o n s t a n t e s

Passo 2

(a)

Agora temos que lembrar que a temperatura para as condições transientes que ocorrem dentro do vaso é regida pela equação 5.25 assim temos:

T = T ∞ + b a 1 - e - a t

Onde.

a = U A s ρ V c ,   b = E ˙ ρ V c = q ˙ ρ c

Devido a presença da parede nosso sistema vai possuir uma resistência térmica a condução e convecção, assim temos da equação 3.19 que U A s = R c o n d + R c o n v - 1 , então vamos calcular nossas resistências?

Das equações 3.9 e 3.41 temos que:

R c o n d = 1 2 π k ⋅ 1 D i - 1 D 0 = 1 2 π ⋅ 17   W m ⋅ K ⋅ 1 1   m - 1 1 , 01   m

R c o n d = 9 , 26 ⋅ 10 - 4   K W

R c o n v = 1 h A 0 = 1 6   W m 2 ⋅ K ⋅ π 1 . 0 1 2

R c o n v = 0,0 52   K W

Assim:

U ⋅ A s = 18 , 89   W K

Passo 3

Agora finalmente podemos calcular a nossa temperatura, sabendo nossas resistências temos que:

a = U A s ρ V c ,   b = E ˙ ρ V c = q ˙ ρ c

Sendo V = π D i 3 6 , temos:

a = 6 ⋅ 18,89 W K 1100 k g m 3 ⋅ π 1 m 3 ⋅ 2400 J k g ⋅ K = 1 , 37 ⋅ 10 - 5   s - 1

b = 10 W m 3 1100 k g m 3 ⋅ 2400 J k g ⋅ K = 3,788 ⋅ 10 - 3   K s

b a = 2 7 6 , 5 ° C

Como a questão pede a temperatura para 5   horas convertendo pra segundos temos:

t = 5 h ⋅ 3600   s h = 18.000   s

Substituindo tudo na nossa equação temos:

T = T ∞ + b a 1 - e - a t

T = 25 ° C + 2 76 , 5 ° C 1 - e - 1 , 37 ⋅ 10 - 5   s - 1 ⋅ 18.000   s =

T = 8 5 , 4   ° C

Passo 4

Agora precisamos calcular a temperatura externa do vaso T s ,   f , se desprezarmos a capacitância térmica do vaso o fluxo de calor na superfície externa por convecção vai ser igual ao fluxo de calor por condução na “casca” do vaso, assim temos:

T - T s ,   f T s ,   f - T ∞ = R c o n d R c o n v = 9,26 ⋅ 10 - 4 K W 0,052   K W = 0,0178

85,4 ° C - T s ,   f T s ,   f - 25 ° C = 0,0178

T s ,   f = 84,3 ° C

Passo 5

(b)

Agora fazendo a equação 5.25 , para duas situações uma com um h pequeno e outra com h grande, que representam respectivamente uma convecção livre e uma convecção forçada, assim nosso gráfico fica.

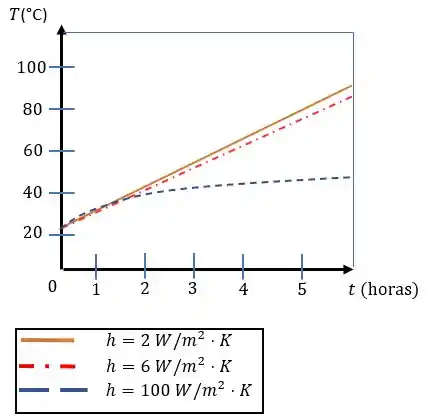
Como podemos observar convecção forçada é mais efetiva no aspecto de reduzirmos a temperatura dos reagentes e chegarmos a um estado de regime estacionário.

Isso é tudo pessoal! Finalmente terminamos!

Resposta

T r e a g e n t e s = 85,4   ° C

T s ,   f = 84,3 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma batata ( ρ = 1.100k g / m 3 ,c p = 3.900J / k g ⋅ K ,k = 0,6W / m ⋅ Keα = 1,4 × 10 - 7m 2 / s ) de 9c m de diâmetro, que está inicialmente a uma temperatura uniforme de 25 ℃ ℃, é assada em um forn
Barras cilíndricas longas de aço inoxidável AISI k = 13,4W / m ⋅ Keα = 3,48 × 10 - 6m 2 / s de 10c m de diâmetro são tratadas termicamente passando à velocidade de 2m / m i n por um forno de 6m de com
Uma pessoa coloca algumas maçãs em um freezer a - 15 ℃ ℃ para esfriá-las rapidamente para os hóspedes que estão prestes a chegar. Inicialmente, as maçãs estão a uma temperatura uniforme de 25 ℃ ℃, e o
Camadas de placas de carne de 15c m de espessura ( k = 0,45W / m ⋅ ℃eα = 1 , 3 × 10 - 7m 2 / s ) ℃ inicialmente a uma temperatura uniforme de 10 ℃ ℃ são refrigeradas por ar a 5 ℃ ℃ para a temperatura
Uma barra de ferro longa ( ρ = 7870k g / m 3 ,c p = 447J / k g ⋅ K ,k = 80,2W / m ⋅ Keα = 23,1 × 10 - 6m 2 / s ) com diâmetro de 25m m é inicialmente aquecida a uma temperatura uniforme de 700 ℃ ℃. A