Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 15

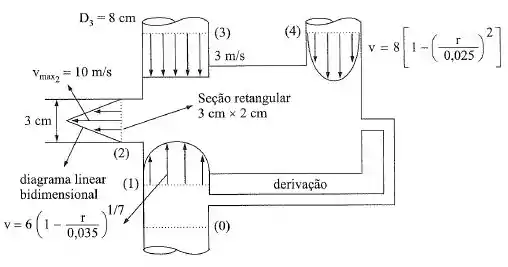
No sistema da figura, tem-se um único fluido incompressível de v = 10 - 4 m 2 / s e ρ = 1000   k g / m 3 .

  1. Qual é o número de R e nas seções 1 e 4 ?
  2. Qual é a velocidade média na seção ( 2 ) ( m / s ) ?
  3. Qual é a vazão em volume nas seções 1 e 4 ( L / s ) ?
  4. Qual é a vazão em volume na derivação e qual o sentido do escoamento? (Indicar no desenho.)
  5. Qual é a vazão em peso na seção ( 0 ) ?
  6. Qual é a velocidade a 1   c m de distância da parede do tubo ( 4 ) ?
  7. Qual é a tensão de cisalhamento na parede do conduto da seção ( 2 ) ?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Item “a”:

Para encontrar o Reynolds na seção 1 e 4 , temos que:

R e = v m D v

Para um escoamento turbulento, temos que:

v m = 49 60   v m á x

E para um escoamento laminar, temos que:

v m = v m á x 2

Portanto:

v m 1 = 49 60   6

v m 1 = 4,9   m / s

E:

v m 4 = 8 2

v m 4 = 4   m / s

Descobertas as velocidades médias podemos encontrar os respectivos números de Reynolds:

R e 1 = v m D 1 v

R e 1 = 4,9 2 0,035 10 - 4

R e 1 = 3430

E:

R e 4 = v m D 2 v

R e 4 = 4 2 0,0 2 5 10 - 4

R e 4 = 2000

Passo 2

Item “b”:

Para encontrarmos a velocidade média no ponto ( 2 ) temos que:

v m 2 = v m á x 2 2

v m 2 = 10 2

v m 2 = 5   m / s

Passo 3

Item “c”:

Para encontrarmos a vazão volumétrica na seção 1 e 4 , temos que:

Q = π R 2 v

Aplicando a cada seção, temos que:

Q 1 = π R 1 2 v 1

Q 1 = π 0,035 2 4,9

Q 1 = 0,0189   m 3 / s

Ou:

Q 1 = 18,9   L / s

E:

Q 4 = π R 4 2 v 4

Q 4 = π 0,0 2 5 2 4

Q 4 = 0,0 078   m 3 / s

Ou:

Q 4 = 7,8   L / s

Passo 4

Item “d”:

Para encontrarmos o valor da vazão na derivação, encontraremos primeiro o valor da vazão em 2 e em 3 :

Q 1 + Q 3 + Q 4 = Q 2 + Q d e r

Portanto:

Q 3 = π D 3 2 4 v 3

Q 3 = π 0,8 2 4 3

Q 3 = 0,0151   m 3 / s

Ou:

Q 3 = 15,1   L / s

E:

Q 2 = A 2 v 2

Q 2 = 5 0,03 0,02

Q 2 = 0,03   m 3 / s

Ou:

Q 2 = 3   L / s

Temos que:

Q d e r = 18,9 + 15,1 + 7,8 - 3

Q d e r = 38,8   L / s

Como o valor da vazão deu positivo, podemos afirmar que esta ocorre para fora.

Passo 5

Item “e”:

A vazão em volumétrica na seção ( 0 ) é dada por:

Q 0 = Q d e r - Q 1

Q 0 = 38,8 - 18,9

Q 0 = 19,9   L / s

A vazão em peso será:

Q G = ρ g Q 0

Logo:

Q G = 1000 10 19,9 10 - 3

Q G = 199   N / s

Passo 6

Item “f”:

A velocidade na distância pedida é dada por:

v = 8 1 - r 0,025 2

v = 8 1 - 0,015 0,025 2

v = 5,12   m / s

Passo 7

A tensão de cisalhamento na parede é dada por:

τ = μ v ε

Onde μ = v ρ , logo:

τ = ( 10 - 4 ⋅ 1000 ) 10 0,015

τ = 66,7   N / m 2

Resposta

a ) R e 1 = 3430

R e 4 = 2000

b ) v m 2 = 5   m / s

c ) Q 1 = 18,9   L / s

Q 4 = 7,8   L / s

d )   Q d e r = 38,8   L / s

e ) Q G = 199   N / s

f ) v = 5,12   m / s

g ) τ = 66,7   N / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O filtro de admissão de combustível de uma certa máquina é formado por um elemento poroso com forma de tronco de cone. O com 10L / s . A distribuição de velocidades na face superior é linear com v m á
O campo de velocidades de um escoamento é dado por v x = 3 y e v y = 2 .O movimento é variado ou permanente?Determinar o campo das acelerações.Determinar os módulos da velocidade e aceleração no ponto
A placa da figura tem uma área de 2m 2 e espessura desprezível. Entre a placa e o solo existe um fluido que escoa formando um diagrama de velocidades bidimensional dado por v = 20 y v m á x ( 1 - 5 y
No sistema da figura, A 3 = 0,5m 2 , ρ 3 = 0,4k g / m 3 e os fluidos são gases. No sistema da figura, o óleo fornecido pela bomba mantém o pistão parado. O óleo escoa através da folga entre o pistão e
O tanque da figura abaixo permanece em nível constante. O escoamento na calha tem uma seção transversal quadrada e é bidimensional, obedecendo à equação v = 3 y 2 . Sabendo que o tanque B tem 1m 3 e é