Um refrigerador residencial opera com reservatórios frio e quente com temperaturas de e, respectivamente. Quando nova, as resistências térmicas nos lados frio e quente são e, respectivamente. Com o tempo, poeira se acumula sobre a serpentina do condensador, localizado na parte de trás do refrigerador, aumentando a resistência no lado quente para. Deseja-se uma taxa de resfriamento no refrigerador de. Usando os resultados do Problema, determine o coeficiente de performance modificado e a alimentação de potência requerida nas condições da serpentina (a) limpa e (b) com poeira.
Passo 1
Essa questão se refere tem o mesmo esquema da questão anterior, porém, ao contrário da outra, essa é numérica. Ilustrativamente, temos que:
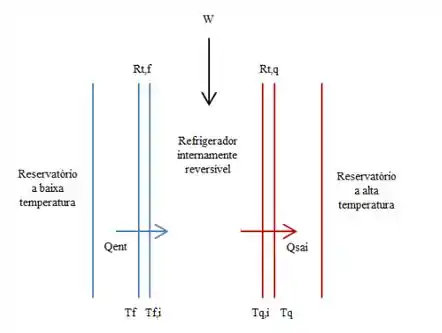
Aqui queremos calcular o coeficiente de performance modificado e a alimentação de potência requerida nas condições da serpentina limpa e com poeira. Então vamos lá!
Passo 2
Vamos primeiro encontrar o coeficiente de performance do refrigerador com a serpentina limpa. Lembrando da questão anterior que a expressão do coeficiente de performance é:
Onde a resistência total é expressa por:
Onde para o caso da letra (a) em que temos a serpentina limpa:
Substituindo os valores na equação de , que o enunciado forneceu (lembrando em converter a unidade da temperatura de °C para K), temos:
Já a potência requerida para o refrigerador pode ser expressa pela seguinte equação:
Substituindo os valores, temos que a potência requerida para serpentina limpa é:
Passo 3
Agora vamos fazer a letra (b), onde teremos a mesma análise anterior, só que dessa vez a serpentina está suja e Então a resistência total é:
E o coeficiente de performance do refrigerador é:
Então, a alimentação de potência requerida é:
Resposta
- e
- e