Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 84
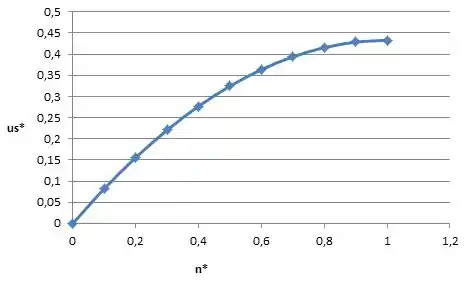
Repita o Exemplo 9–17, coma diferença de que a parede é inclinada no ângulo (Fig. P9–89). Encontre expressões para os campos de pressão e velocidade. Como verificação certifique – se que o seu resultado concorda com o do Exemplo 9–17 quando um . [Dica: É mais conveniente usar o sistema de coordenadas com componentes de velocidade , onde y está para dentro da página na Fig. P9-84. Desenhe o perfil de velocidade adimensional versus no caso no qual ]
Passo 1
Animados para continuar??
Eu espero que siiim !!
Vamos ter que fazer algumas observações, ok?
O problema já nos disse que o escoamento é permanente e incompressível !!
Sabemos pelo problema que o escoamento é constante, ou seja, as derivadas com relação ao tempo são iguais a zero !!
Também vimos que o escoamento é paralelo, o que isso nos diz? Que a componente n da velocidade, é igual a zero em todos os lugares !!
Se o escoamento ocorre apenas com relação ao eixo não há velocidade na direção , ou seja, assim como todas as suas derivadas parciais !!
E para finalizar nossos comentários, que são muitíssimos úteis (não se deixem enganar pela preguiça !) existe a força gravitacional no sentido negativo de z, lembrando da trigonometria:
Beleza !! Agora nós podemos começar lembrando da equação da continuidade:
As componentes da velocidade são dadas pelo problema, não é verdade?
Podemos substituir:
Para satisfazer a equação de Bernoulli a componente da velocidade não pode variar com relação a s, nem com relação a y, certo? Já que nós não estamos trabalhando com o eixo aqui !!
Então a única opção é que varie com relação a ou melhor,
Passo 2
Se a equação da continuidade é satisfeita nós podemos usar a equação de Navier – Stokes.
Para a direção n, nós temos que:
Como
Integrando:
E agora? O que faremos?
Precisamos achar esta constante de integração que apareceu e, por isso, vamos usar nossa tão querida condição de contorno!!
Passo 3
Segundo a figura, na superfície livre, ou seja, quando teremos :
E agora é só colocar na pressão:
Podemos conferir nossa equação para o Exemplo 9-17, quando :
Comprovando o que achamos, certo?
Então para a pressão nós já achamos !! Vamos para a velocidade?
Aqui nós vamos analisar a componente na direção s:
Se só varia com relação a n:
E lembrando que na direção n não vai haver gradiente de pressão:
Então:
Integrando a primeira vez:
Integrando a segunda vez:
E agora? O que faremos?
Precisamos achar estas constantes de integração que apareceram e, por isso, vamos usar nossa tão queridas condições de contorno!!
Passo 4
Segundo a condição de contorno antiderrapante, as paredes do tanque são estacionárias, ou seja, quando não há velocidade:
Já na superfície livre, , não há tensão de cisalhamento:
Substituindo a condição de contorno para :
E colocando a segunda condição:
Substituindo o valor das constantes na componente da velocidade:
Passo 5
Achamos a velocidade, mas também queremos o perfil em termos adimensionais!!
Para isso vamos começar reorganizando esta equação:
Chamando:
Substituindo:
Quando
Como os valores máximos para são e , teremos que:
Substituindo na fórmula:
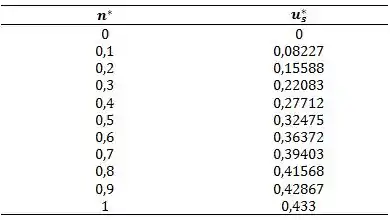
Agora é só fazer um gráfico bem bonito e descobriremos o perfil da velocidade:
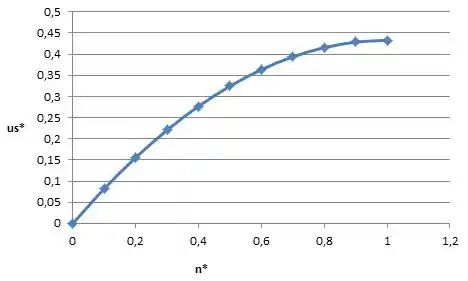
E chegamos ao fim de mais uma beem legal !!
Resposta
