Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 147
Repita o Problema P3.49, considerando que p1 seja desconhecida e usando a equação de Bernoulli (sem perdas). Calcule a nova força sobre os parafusos com essa hipótese. Qual é a perda de carga entre 1 e 2 para os dados do Problema 3.49?
Passo 1
Bora pra mais uma!
Vamos relembrar o enunciado do problema 3.49:
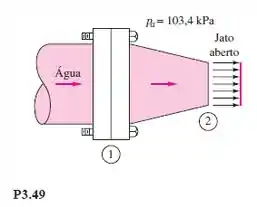
O bocal horizontal da Figura P3.49 tem D1 300 mm e D2 = 150 mm, com pressão de entrada p1 = 262 kPa absoluta e V2 = 17 m/s. Para água a 20C, calcule a força horizontal fornecida pelos parafusos dos flanges para manter o bocal fixo.
Temos que:
Vamos aplicar a equação de Bernoulli sem considerar perdas de carga, e considerando pontos 1 e 2 sob mesma altura. Daí:
Então obtemos:
Passo 2
Agora, vamos analisar as forças que atuam sobre nosso volume de controle, conforme a segunda lei de Newton, se formos analisar nosso volume de controle o somatório das forças deverá ser igual a zero.
Considerando um referencial de eixos com o eixo X positivo apontado para a direita, temos que as forças que atuam sobre o nosso volume de controle são:
Sendo que a vazão mássica é:
Então:
Por fim, podemos estimar a perda de carga por atrito pela equação da energia de forma utilizando o valor de p1 = 262 kPa enunciado no exercício 3.49:
Resposta
A perda de carga entre 1 e 2 para os dados do Problema 3.49 é de 5,16m. E a nova força sobre os parafusos é de .