Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 54
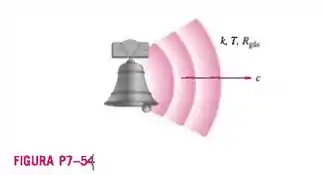
Sabe-se que a velocidade do som c em um gás ideal é uma função da razão entre os calores específicos , da temperatura absoluta e da constante específica do gás ideal (Figura P7-54). Mostrando todo o seu trabalho, use a análise dimensional para encontrar a relação funcional entre esses parâmetros.
Passo 1
Então a gente tem que achar uma relação entre a velocidade do som com a razão dos calores específicos (), a temperatura absoluta () e a costante específica do gás ideal ().
Não tem problema nenhum não lembrar dessa parte da física, eu também não lembro haha!
Aqui vamos usar o método das variáveis repetidas para resolver esse problema!
Então vamos começar com o primeiro passo que é listar os parâmetros relevantes que o enunciado da pra a gente!
Temos então parâmetros relevantes!!
Passo 2
Agora a gente precisa listar as dimensões primárias de cada parâmetro!
O enunciado diz que é uma RAZÃO dos calores específicos, então a gente imagina que é uma divisão entre dois calores específicos diferentes, mas se temos calor específico em cima e calor específico em baixo, as unidades de cancelam, logo é adimensional.
Passo 3
Como nossos parâmetros são descritos por dimensões básicas () o primeiro chute de
Substituindo no teorema de Pi de Buckingham:
Devemos esperar um único grupo !
Passo 4
Já que vamos considerar precisamos encontrar nossos três parâmetros repetidos!
Relembrando nossos parâmetros:
De cara a gente já sabe que a gente não pode usar, pois ele é um parâmetro dependente!
Sobra pra a gente e , o problema é que não tem dimensão então não podemos usar ele.
Passo 5
Vamos reduzir para
Dessa forma:
Nosso palpite é que agora tem grupos e as variáveis repetidas serão e .
Passo 6
Agora sim, vamos encontrar o nosso primeiro grupo . Começando com o que vai ser o dependente!
Organizando os nossos parâmetros a gente fica com:
Escrevendo suas dimensões básicas:
Agora equacionando:
Comprimento:
Tempo:
Temperatura:
Substituindo e temos:
Organizando:
Agora deveriamos achar que é uma função das variáveis repetidas com k
Porém, como é adimensional, então os expoentes e deverão ser igual a zero, com isso:
Passo 7
Escrevendo a relação entre os grupos :