Seja o escoamento laminar de um fluido com Pr = 4, com uma vazão, que passa por um processo de entrada combinada, com uma temperatura superficial constante, em um tubo com comprimento L

Vamo analisar o enunciado junto pra entender o que ele quer de você.

Temos um fluido com número de Prandtl constante , com temperatura superficial constante em um tubo de comprimento e vazão mássica escoando em um processo de entrada combinada como mostra o esquema abaixo:

Um engenheiro sugere que o tubo seja dividido em tubos de mesmo comprimento e vazão mássica , como mostra esse outro esquema aí embaixo:

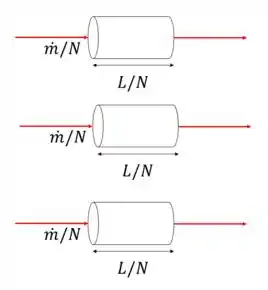
Devemos encontrar, então, uma relação entre o coeficiente de transferência de calor média depois da divisão dos tubos e o coeficiente do tubo original.

Para fazer isso, antes a gente tem que lembrar algumas definições.

Primeiro devemos lembrar que o número de Nusselt para um um processo de entrada combinada é:

Sendo e os adimensionais conhecidos, respectivamente, como números de Prandtl e Graetz. Essa correlação é válida para um valor de temperatura superficial constante e .

Dessa maneira, o número de Nusselt pode ser entendido como uma função dos números de Graetz e Prandtl, como segue:

Esses adimensionais podem ser calculados da seguinte forma:

Sendo a o diâmetro do tubo, o comprimento do tubo orginal, a viscosidade dinâmica, o calor específico e a condutividade térmica.

Por fim, o número de Reynolds pode ser calculado como:

Sendo a velocidade de escoamento, o diâmetro do tubo e a viscosidade cinemática.