Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 75

Lembre-se da placa retangular bidimensional do Problema 4.2. Usando um método numérico apropriado, com Δx = Δy = 0,25 m, determine a temperatura no seu ponto central (1; 0,5).

Passo 1

Então turminhaa, animados para mais umaa ?!

Vamos começar desenhando nossa placa do Problema 4.2, com Δx = Δy = 0,25 m:

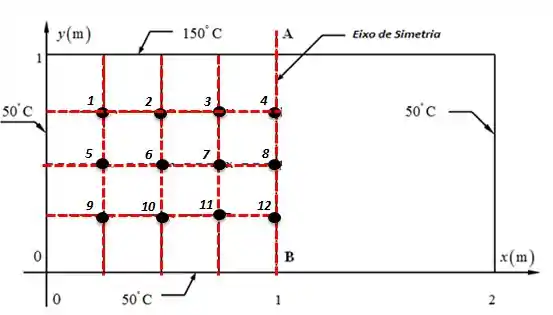
O que nós vemos aqui é os pontos de 1 até 12 são nós internos, então a formula nestes casos é:

4 T m , n = ∑ T v i z i n h o s

Fazendo para cada ponto:

4 T 1 = T 2 + T 5 + 200

4 T 2 = T 1 + T 3 + T 6 + 150

4 T 3 = T 2 + T 4 + T 7 + 150

4 T 4 = 2 T 3 + T 8 + 150

4 T 5 = T 1 + T 6 + T 6 + 50

4 T 6 = T 2 + T 5 + T 7 + T 10

4 T 7 = T 3 + T 4 + T 8 + T 11

4 T 8 = 2 T 7 + T 4 + T 12

4 T 9 = T 5 + T 10 + 100

4 T 10 = T 6 + T 9 + T 11 + 50

4 T 11 = T 7 + T 10 + T 12 + 50

4 T 12 = 2 T 11 + T 8 + 50

Quando resolvemos as equações simultâneas com ajuda do nosso amado software:

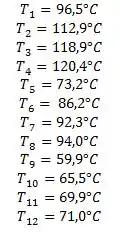
Mas o que nós queremos é a temperatura no ponto central, ( 1 ,   0,5 ) , certo?

Este ponto nós chamamos de ponto 8:

T 1 ,   0,5 = T 8 = 94,0 ° C

Aaaaa agora siiim!!

Vamos pro próximo?!

Resposta

T 1 ,   0,5 = T 8 = 94,0 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa unidimensional com espessura 2 L está inicialmente a uma temperatura uniforme T i . Subitamente, uma corrente elétrica é passada através da placa, causando um aquecimento volumétrico uniform
Uma parede, com 0,12m de espessura e difusividade térmica de 1,5×10 - 6m 2/ s , encontra-se inicialmente a uma temperatura uniforme igual a 85 ° C . Subitamente, uma de suas faces tem a sua temperatur
Um cilindro sólido redondo, feito com um material plástico ( α=6 × 10 - 7 m 2 / s ) , está inicialmente a uma temperatura uniforme de 20 ° C e se encontra isolado ao longo de sua superfície lateral e
Seja o Problema 5.9, exceto pelo fato de que agora o volume combinado do banho de óleo e da esfera é igual a V=1m 3 . O banho de óleo é bem misturado e isolado termicamente. (a) Considerando que as pr
Uma parede plana ( ρ=4000k g / m 3,c p=500J / ( k g·K ) ,k=10W / ( m·K ) ) , com espessura L=20m m , tem inicialmente uma distribuição de temperaturas estacionária linear, com as superfícies mantidas