Uma placa de grande espessura, com difusividade térmica de e condutividade térmica de , está inicialmente a uma temperatura uniforme de . De repente, a sua superfície é exposta a uma substância refrigerante a , que mantém um coeficiente de transferência de calor por convecção igual a . Usando o método de diferenças finitas com um incremento espacial de e um incremento no tempo de , determine as temperaturas na superfície e a uma profundidade de , passados do início do processo.
Passo 1
Vamos lá! Nosso problema pede a temperatura na superfície e na profundidade de , mas antes vamos fazer um esboço para facilitar nossa vida.
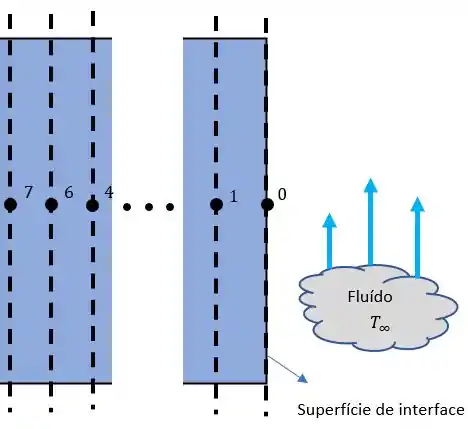
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
Vamos lá, com nossos dados em mãos vamos calcular a distribuição de temperatura pelo método das diferenças finitas, como foi sugerido pelo problema, para o ponto podemos usar a equação para as condições unidimensionais ou a . Então temos:
Agora calculando os números e , vamos ter:
Substituindo os dados na equação para :
Passo 3
Agora Temos que lembrar que precisamos atender o critério de estabilidade:
Organizando
Substituindo:
Logo o nosso critério de estabilidade é atendido, assim usando a equação para os nós internos, a equação vai ficar assim.
Substituindo temos:
Passo 4
Agora vamos fazer uma tabela com intervalos de 18 segundos, para um tempo total de , mas antes vamos calcular a quantidade de pontos, sendo assim:
Por fim nossa tabela fica assim:
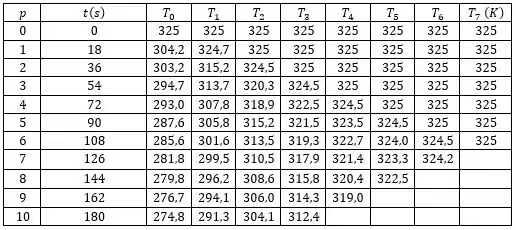
Como o problema pede a temperatura na superfície de interface e na profundidade de , temos:
Isso é tudo pessoal! \o/
