Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 73

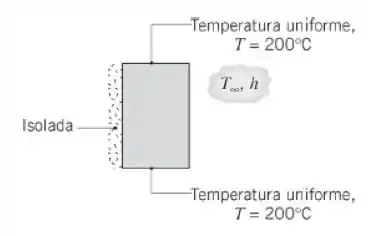
Uma longa barra, com seção transversal retangular, 0,4   m   ×   0,6   m , e condutividade térmica igual a 1,5 W m K , está sujeita às condições de contorno mostradas na figura. Duas das laterais são mantidas a uma temperatura uniforme de 200°C. Uma das laterais é adiabática e o lado restante está sujeito a um processo convectivo com T ∞   =   30 ° C e h   =   50 W m 2 K . Usando uma técnica numérica apropriada, com uma malha com espaçamento de 0,1 m, determine a distribuição de temperaturas na barra e a taxa de transferência de calor entre a barra e o fluido, por unidade de comprimento da barra.

Passo 1

Boom galerinha, vamos começar?

Vamos começar desenhando o que está acontecendo neste problema:

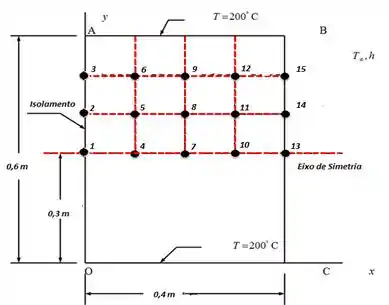
O que nós vemos aqui é os pontos de 1 até 12 são nós internos, então a formula nestes casos é:

4 T m , n = ∑ T v i z i n h o s

Fazendo para cada ponto:

4 T 1 = 2 T 2 + 2 T 4

4 T 2 = T 1 + 2 T 5 + T 3

4 T 3 = T 3 + 2 T 6 + 200

4 T 4 = T 1 + 2 T 5 + T 7

4 T 5 = T 2 + T 6 + T 8 + T 4

4 T 6 = T 5 + T 3 + T 9 + 200

4 T 7 = T 4 + 2 T 8 + T 10

4 T 8 = T 7 + T 5 + T 9 + T 11

4 T 9 = T 8 + T 6 + T 12 + 200

4 T 10 = T 7 + 2 T 11 + T 13

4 T 11 = T 10 + T 8 + T 12 + T 14

4 T 12 = T 11 + T 9 + T 15 + 200

Para os pontos de 13 até 15:

2 T m - 1 , n + T m , n + 1 + T m , n - 1 + 2 h ∆ x k T ∞ - 2 h ∆ x k + 2 T m , n = 0

Sabendo que:

T ∞ = 30 ° C

h = 50 W m 2 K

k   =   1,5 W m K

∆ x = 0,1   m

Substituindo:

2 T m - 1 , n + T m , n + 1 + T m , n - 1 + 200 = 10,67 T m , n

Colocando os pontos:

2 T 10 + T 14 + 200 = 10,67 T 13

2 T 11 + T 13 + T 15 + 200 = 10,67 T 14

2 T 12 + T 14 + 200 + 200 = 10,67 T 15

Quando resolvemos as equações simultâneas com ajuda do nosso software:

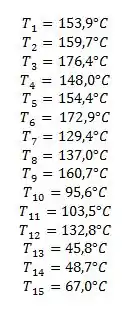
Passo 2

Mas o que nós queremos é o calor, certo?

Como nós temos duas partes iguais e o calor por convecção é perdido pelos pontos 13, 14, 15 e no ponto onde a temperatura é de 200°C

q c o n v = 2 h ∆ y T 13 - T ∞ 2 + T 14 - T ∞ + T 15 - T ∞ + T s - T ∞ 2

q c o n v = h ∆ y T 13 + 2 T 14 + 2 T 15 + T s - 6 T ∞

q c o n v = 50 W m 2 K 0,1   m 45,8 ° C + 2 48,7 ° C + 2 67,0 ° C + 200 ° C - 6 30 ° C

q c o n v = 1487 W m

E ficamos por aqui galerinhaa !!

Resposta

q c o n v = 1487 W m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas barras muito longas (na direção normal à página) com as distribuições iniciais de temperaturas mostradas na tabela, devem ser soldadas lateralmente uma à outra. No tempo t=0 , a face equivalente
O critério de estabilidade para o método explícito exige que o coeficiente do termo T m p na equação de diferenças finitas unidimensional seja zero ou positivo. Analise a situação na qual as temperatu
Deduza a equação de diferenças finitas, bidimensional e transiente, para a temperatura no ponto nodal 0 localizado sobre a fronteira entre dois materiais diferentes.
Um fino bastão com diâmetro D está inicialmente em equilíbrio com a sua vizinhança, um grande recipiente, onde há vácuo, a uma temperatura T v i z . De repente, uma corrente elétrica I ( A ) é passada
Deduza uma equação de diferenças finitas explícita para um nó interior para a condução tridimensional transiente. Também determine o critério de estabilidade. Suponha propriedades constantes e espaçam